Erzeugung von Röntgenstrahlung
Aus einer beheizten Glühkathode der RÖNTGEN-Röhre treten freie Elektronen aus (Glühelektrischer Effekt). Durch eine hohe Spannung zwischen Glühkathode und Anode werden diese freien Elektronen sehr stark zur Anode hin beschleunigt. Bei der Wechselwirkung der schnellen Elektronen mit dem Material der Anode beim Auftreffen wird elektromagnetische Strahlung im RÖNTGEN-Bereich erzeugt.
Ausführlichere Informationen über RÖNTGEN-Röhren erhältst du hier.
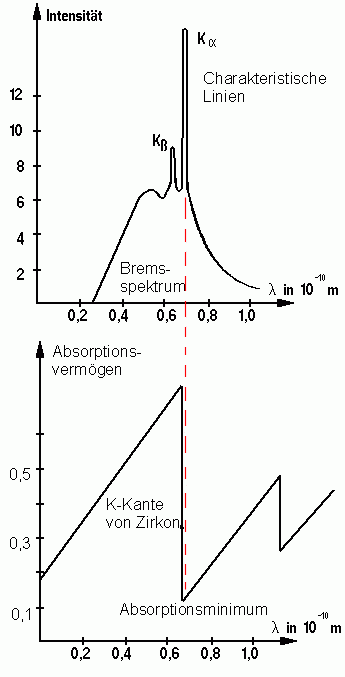
Spektrum einer Röntgenröhre
Ohne besondere Maßnahmen emittiert eine Röntgenröhre sogenannten "weißes Röntgenlicht", d.h. Röntgenstrahlung, die sich über einen größeren Wellenlängenbereich erstreckt. Das Röntgenspektrum besteht aus zwei Anteilen, dem Bremsspektrum und dem charakteristischen Spektrum:
- Bremsspektrum:
Das Bremsspektrum ist unabhängig vom Anodenmaterial und besitzt eine von der Beschleunigungsspannung abhängige Grenzwellenlänge. Im Beispiel in Abb. 2 oben beträgt \(\lambda_{\rm{gr}}=0{,}25\cdot 10^{-10}\,\rm{m}\).
- Charakteristisches Spektrum:
Das charakteristische Spektrum ist insbesondere vom Anodenmaterial abhängig, seiner grundsätzlichen Form mit verschiedenen Spitzen aber nahezu unabhängig von der Anodenspannung. Besonders intensiv ist die sog. \(K_{\alpha}\)-Linie des charakteristischen Spektrums.
Herstellung monochromatischer Röntgenstrahlung
Um "einfarbiges" Röntgenlicht, d.h. Röntgenstrahlung mit einer bestimmten Wellenlänge zu erhalten, kannst du nicht wie in der Optik mit einem gläsernen Farbfilter arbeiten. Man benutzt stattdessen bestimmte Metallfolien deren Absorptionsvermögen bei der Wellenlänge der \(K_{\alpha}\)-Linie besonders schwach ist, also viel Röntgenstrahlung dieser Wellenlänge durchlässt und deren Absorptionsvermögen in der Umgebung der \(K_{\alpha}\)-Linie stark zunimmt.
Für das in Abb. 2 oben gezeigte Spektrum eignet sich z.B. Zirkonium als Filtermaterial (siehe Abb. 2 unten). Zirkonium absorbiert im Bereich der \(K_{\alpha}\)-Linie besonders schlecht.
Versuchsaufbau der Drehkristallmethode von Bragg
Aus den aus der Anode austretenden Röntgenstrahlen wird mit Hilfe zweier Bleiblenden ein feines Bündel an Röntgenstrahlen erzeugt.
Durch einen Zirkonfilter wird praktisch nur die für das Anodenmaterial Molybdän charakteristische \(K_{\alpha}\)-Linie durchgelassen (siehe oben), Röntgenstrahlung anderer Wellenlänge wird absorbiert. Das feine monochromatische Bündel an Röntgenstrahlen trifft unter einem variablen Drehwinkel \(\theta\) auf einen Einkristall, an dessen Atomen die Röntgenstrahlung gebeugt bzw. "reflektiert" wird. Der gebeugte bzw. "reflektierte" Strahl wird mit einem Zählrohr analysiert, wobei die ermittelte Zählrate ein Maßstab für die Intensität der Röntgenstrahlung unter dem Winkel \(\theta\) ist.
Beobachtung im Versuch
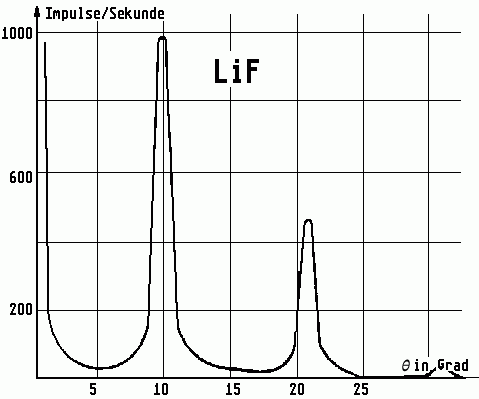
Unter mehreren Einfallswinkeln \(\theta\) zeigen sich ausgeprägte Maxima der Impulsrate, während zwischen diesen Winkeln jeweils kaum Impulse gezählt werden. Abb. 5 zeigt ein entsprechendes Diagramm bei Nutzung eines Lithium-Fluorid-Kristalls.
Deutung
Die auf den Kristall treffende, monochromatische Röntgenstrahlung wird vom Kristall nur unter bestimmten Drehwinkeln \(\theta=90^{\circ}-\alpha\) gebeugt bzw. "reflektiert". Unter diesen Drehwinkeln \(\theta\) tritt konstruktive Interferenz zwischen den Röntgenstrahlen auf, die an zwei unterschiedlichen Netzebenen im Abstand \(d\) des Kristalls "reflektiert" werden.
In diesen Fällen erfüllen die experimentellen Parameter die Bragg-Bedingung \(n\cdot \lambda=2\cdot d\cdot \sin\left(\theta\right)\).
Im Graph zeigen sich zwei ausgeprägte Maxima. Dabei handelt es sich bei \(\theta_1=10{,}3^{\circ}\) um das Maximum 1. Ordnung (\(n=1\)) und bei \(\theta_2=21^{\circ}\) um das Maximum der 2. Ordnung (\(n=2\)).
Hinweis: Andere Kristalle besitzen mehr als einen Netzebenenabstand \(d\). So besitzt z.B. die hexagonale Kristallstruktur von Graphit zwei unterschiedliche Netzebenenabstände \(d_1\) und \(d_2\). Es zeigen sich entsprechend für beide Netzebenenabstände Glanzwinkel.
Aufgabe
Für einen Lithium-Fluorid-Kristall kennt man den Netzebenenabstand \(d = 2{,}01\cdot 10^{-10}\,\rm{m}\). Bestimme aus den in Abb. 5 dargestellten Messwerten die Wellenlänge der durch den Zirkonfilter herausgefilterten charakteristischen \(K_{\alpha}\)-Linie des hier genutzten Anodenmaterials Molybdän.
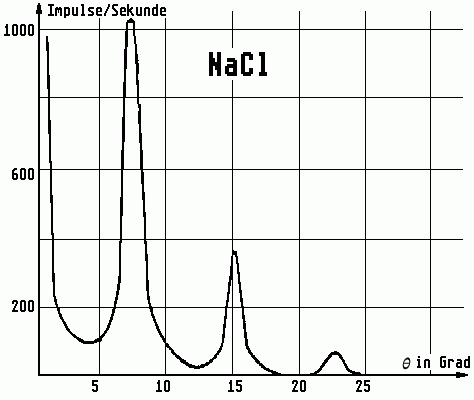
Bestimme aus dem in Abb. 6 dargestellten Diagramm den Gitterabstand des NaCl-Kristalls.