|
Aufbau
|
Schirmbild
|
Theorie
|
Bemerkungen
|
Details:
|
|
Theoretische Behandlung wie beim Doppelspalt:
Gangunterschied:
\[ \Delta s = b \cdot \sin{\alpha} \]
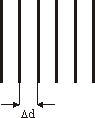
Abstand benachbarter Maxima am Schirm:
\[ \Delta d = \frac{\lambda \cdot a}{b} \]
-
a: Abstand der virtuellen Quellen vom Schirm;
-
b: Abstand der virtuellen Quellen;
-
λ: Wellenlänge des Lichts;
-
α: Winkel zwischen optischer Achse und dem Strahl zum Beobachtungspunkt auf dem Schirm;
|
- Zweiquelleninterferenz in Querbeobachtung;
- Bestimmung des Abstandes b durch Linsenabbildung; (vgl. Müller, Leitner II, Seite 136/5);
- Bei Verwendung von weißem Licht treten Farbsäume an den Maxima auf, deren Ordnung von Null verschieden ist;
- Nur ein sehr flaches Prisma (großer Öffnungswinkel) führt zur Kohärenz;
- Analogieexperiment: Versuch von Möllenstedt und Düker mit "Elektronenwellen";
|
Versuchsaufbau

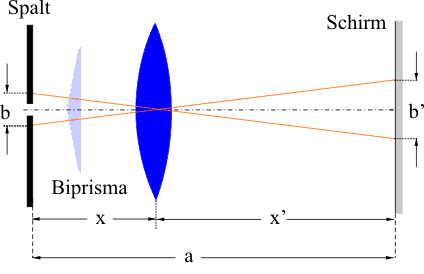
Anordnung mit Objektiv zur Bestimmung des Abstands b der beiden virtuellen Lichtquellen
|
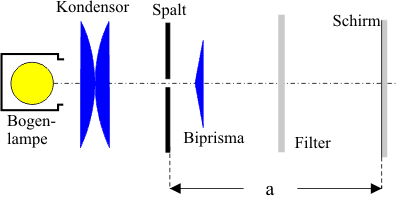
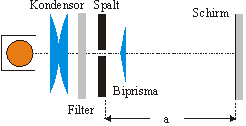
Anordnung ohne Objektiv zur Darstellung der Interferenzfigur
|
Zur Justierung der Anordnung
- Zunächst wird mit der starken Lichtquelle (Kohlebogenlampe) das Licht durch einen Kondensor auf den sehr engen senkrechten Kohärenzspalt gebündelt.
- Dann wird mit einem Objektiv der Kohärenzspalt scharf auf einen etwa a = 5,00 m entfernten Schirm abgebildet.
- Nun bringt man etwa 10 cm hinter dem Kohärenzspalt das Biprisma und schiebt es so genau in den Strahlengang, dass am Schirm aus dem einen Spaltbild zwei Spaltbilder werden.
- Aus dem Abstand dieser Spaltbilder b´, dem Abstand Schirm - Objektiv x´ und dem Abstand Objektiv Kohärenzspalt bestimmt man den Abstand b der beiden virtuellen Kohärenzspalte.
\[ \frac{b}{b'} = \frac{x}{x'} \Rightarrow b = b' \cdot \frac{x}{x'} \]
|
|
- Anschließend bringt man ein Farbfilter in den Strahlengang, so dass die beiden Spaltbilder farbig werden.
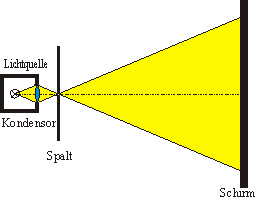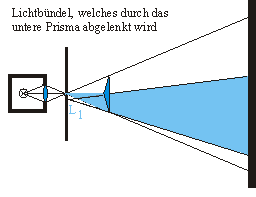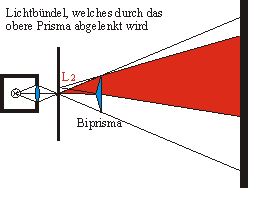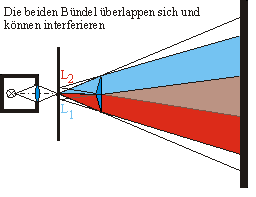
- Entfernt man nun das Objektiv, so kann man an der Stelle der bisherigen Spaltbilder Interfernzfiguren wie beim Doppelspaltversuch sehen und entsprechend wie beim Doppelspaltversuch die Wellenlänge bestimmen.
|
|
Biprisma - Überlappung
Theoretische Behandlung des Biprismaversuchs
|
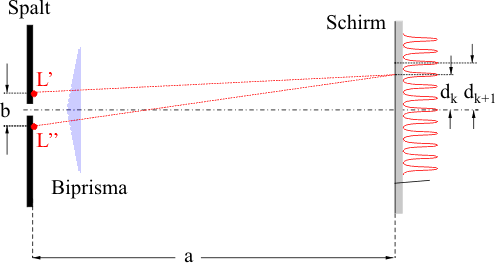
Für den Gangunterschied Δs der von L' und L'' ausgehenden Wellen gilt:
\[\Delta s = b \cdot \sin \left( \alpha \right)\]
|
\(\alpha\):
|
Winkel zwischen optischer Achse und dem Strahl zum Beobachtungspunkt auf dem Schirm;
|
Für das k-te Maxima gilt
\[k \cdot \lambda = b \cdot \sin \left( \alpha \right)\]
und für \({\alpha \, \ll \,1}\) (Kleinwinkelnäherung)
\[k \cdot \lambda \approx b \cdot \tan \left( \alpha \right) = b \cdot \frac{{{d_k}}}{a}\]
Analog gilt für das k+1-te Maximum:
\[ (k + 1) \cdot \lambda \approx b \cdot \frac{d_{k+1}}{a} \]
Für den Abstand Δd benachbarter Maxima folgt daher:
\[ \Delta d = d_{k+1} - d_k \\\\
\Delta d = \frac{\lambda \cdot a}{b} \]
|
|