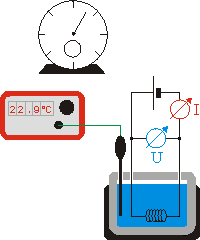
In der folgenden Versuchsserie wird gezeigt, wie man experimentell die Abhängikeit der elektrischen Arbeit von naheliegenden Einflussgrößen untersuchen kann. Dabei werden Methoden angewandt, die exemplarisch für das physikalische Vorgehen zur Gewinnung eines Gesetzes sind.
Hinweis: Das Vorgehen bei diesem Versuch setzt die Formel für die Änderung der inneren Energie bei Temperaturänderung voraus.
Wenn man darüber nachdenkt, von welchen physikalischen Größen die elektrische Arbeit abhängt, so kommt man unschwer auf die Idee, dass der elektrische Strom, die Spannung und auch die Zeitdauer, während der die elektrische Quelle eingeschaltet ist, eine Rolle spielen könnten. Wie die elektrische Arbeit genau von diesen Einflussgrößen abhängt soll der folgende Versuch zeigen.
Rückblick: Im Laufe des Physikkurses standen wir schon einmal vor einem ähnlichen Problem: Gesucht war die Formel für die Bewegungsenergie (kinetische Energie) eines Körpers: \({E_{kin}} = {\textstyle{1 \over 2}} \cdot m \cdot {v^2}\). Du brauchst dich an Details des damals durchgeführten Versuchs nicht mehr erinnern, Du solltest aber noch wissen, dass wir damals die Bewegungsenergie eines Körpers in Lageenergie (potenzielle Energie) umgewandelt haben, von der wir bereits die Formel \({E_{pot}}=m \cdot g \cdot h\) kannten.
Zum Auffinden der Formel für die elektrische Arbeit wandeln wir elektrische Energie einer Quelle in eine Energieform um, bei der du dich schon gut auskennen solltest, der inneren Energie Ei. Durch einen Tauchsieder wird elektrische Energie der Quelle nahezu vollständig in innere Energie der Flüssigkeit gewandelt, in der sich der Tauchsieder befindet. Die elektrische Arbeit Wel ist bei Verlustlosigkeit gleich der Zunahme der innere Energie ?Ei der Flüssigkeit:\[{W_{el}} = \Delta {E_i}\quad (1)\]Damit die innere Energie des Wassers nicht gleich an die Umgebung abgegeben wird, verwendet man bei diesem Versuch ein gutes Kalorimeter.
Abhängigkeit von der Zeit
Bei diesem Versuch lässt man die beiden andern vermuteten Einflussgrößen (U und I) konstant.
 |
|
|
Messergebnisse: Für mw = 200g; U = 2,6V und I = 2,5A ergibt sich:
| t in min | 0 | 1 | 2 | 3 | 4 |
| \(\vartheta \) in °C | 22,9 | 23,3 | 23,8 | 24,3 | 24,7 |
| \(\Delta \vartheta \) in °C | 0 | 0,4 | 0,9 | 1,4 | 1,8 |
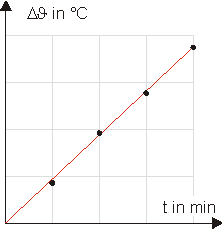
Zeichne das zugehörige \(t\)-\(\Delta \vartheta \)-Diagramm und formuliere die Abhängigkeit der Temperaturänderung von der Zeit.
Die Proportionalitätsbeziehung \(\Delta \vartheta \sim t\) kann einseitig mit konstanten Werten multipliziert werden. Hier multipliziert man die linke Seite mit den konstanten Werten mw und cw:\[{c_{\rm{w}}} \cdot {m_{\rm{w}}} \cdot \Delta \vartheta \sim t\quad {\rm{ oder}}\quad {\rm{ }}\Delta {E_i} \sim t\]Wegen unserer Annahme auf der Eingangsseite, dass die Zunahme der inneren Energie gleich der elektrischen Arbeit ist \({W_{el}} = \Delta {E_i}\)(1), gilt dann\[{W_{el}} \sim t\quad (2)\]wenn U und I konstant gehalten werden.
Abhängigkeit von der Spannung
Für diese Untersuchung müsste die Spannung variiert werden, während die beiden anderen Einflussgrößen Strom und Zeit festgehalten werden. Es zeigt sich nun, dass bei der Verwendung einer Wendel bei einer Spannungserhöhung auch der Strom größer wird. Hier hilft ein kleiner Trick weiter. Schaltet man z.B. zwei Heizwendeln in Serie, so braucht man um wieder - wie beim 1. Versuch - den Strom von 2,5A zu bekommen die doppelte Spannung. Also gelingt es uns auf diese Weise den Strom konstant zu halten und die Spannung zu verdoppeln. Die folgende Animation soll ihnen dies auch plausibel machen.
Fügt man die beiden gleichartigen, zunächst getrennten Kreise zusammen, so zeigt sich, dass die Leitung in der Mitte überflüssig ist, da in ihr insgesamt die Stromstärke Null ist. Man kann die Leitung also entfernen.
In dem so entstandenen Stromkreis ist die Stromstärke genauso hoch wie in den Einzelkreisen, die Spannung ist aber doppelt so hoch.
|
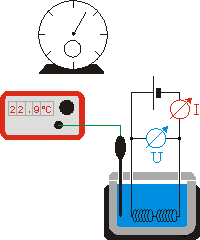
U = 5,2V und I = 2,5A
Im Vergleich zum ersten Versuch ist die Erwärmung bei gleicher Zeitspanne und gleichem Strom doppelt so hoch. Natürlich müsste man den Versuch auch noch mit drei, vier usw. Spulen durchführen, die in Serie geschaltet sind. Man kann jedoch aufgrund der Messergebnisse bei zwei in Serie geschaltete Spulen schon vermuten: \[\Delta \vartheta \sim U\] Multipliziert man wie nun wieder mit den konstanden Größen cw und mw, so erhält man: \[{c_{\rm{w}}} \cdot {m_{\rm{w}}} \cdot \Delta \vartheta \sim U\] oder \[{W_{el}} \sim U\quad (3)\]wenn t und I konstant gehalten werden |
 |
Abhängigkeit von der Stromstärke
|
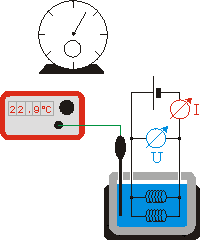
Bei der Parallelschaltung der Heizspiralen liegt die Spannung (2,6 V) von Versuch 1 sowohl an der oberen als auch an der unteren Spirale an. Durch jede Spirale fließt dann der gleiche Strom (2,5 A) wie im ersten Versuch. In der Hauptleitung ist dann aber die doppelte Stromstärke festzustellen: U = 2,6 V und I =5,0 A
wenn t und U konstant gehalten werden |
 |
Zusammenfassung
Aus Wel ~ t (2); Wel ~ U (3) und Wel ~ I (4) folgt:
Wel ~ U · I · t oder Wel = k · U · I · t
Wenn Du beim Zusammenfassen von Proportionalitäten Schwierigkeiten hast, so gehe zu der folgenden Seite.
Für den Proportionalitätsfaktor k ergibt sich\[k = \frac{{{W_{el}}}}{{U \cdot I \cdot t}}\quad {\rm{mit}}\quad \left[ k \right] = \frac{{\rm{J}}}{{{\rm{V}} \cdot {\rm{A}} \cdot {\rm{s}}}}\]Beim Einsetzen der gemessenen Werte liegt der Zahlenwert für k nahe bei 1. Aufgrund der Spannungsdefinition gilt: 1 J = 1 V·A·s. Somit ist die Konstante k dimensionslos und hat bei sehr genauen Messungen den Wert 1. Es gilt also\[{W_{el}} = U \cdot I \cdot t\]