Aufbau und Durchführung


Eine Kugel wird an einem Faden aufgehängt. Eine Rasierklinge wird so angebracht, dass sie den Faden kurz oberhalb der Kugel berührt. Man zieht die Kugel aus der Waagerechten, so dass sie sich um die Höhe \(h\) hebt, und lässt dann los.
Zunächst wird die Lageenergie der Kugel in Bewegungsenergie umgesetzt. Sowie der Faden die Rasierklinge erreicht wird er durchtrennt, die Kugel führt einen waagerechten Wurf durch, durchfällt dabei die Höhe \(y\) und trifft im Abstand \(x\) vom Durchschneidepunkt auf ein am Boden befestigtes Papier. Auf das Papier hat man ein Stück Kohlepapier gelegt, damit der Auftreffpunkt markiert wird.
Beobachtung
Die Animation in Abb. 2 zeigt den Aufbau, die Durchführung und die Beobachtung des Rasierklingenversuchs.
Auswertung
Aufgabe
Drücke die Geschwindigkeit \(v\) der Kugel beim Durchtrennen des Fadens mit der Rasierklinge durch die Höhe \(h\) aus.
Drücke die Weite \(x\) durch die Tiefe \(y\) und die Geschwindigkeit \(v\) aus und anschließend \(x\) durch \(y\) und \(h\).
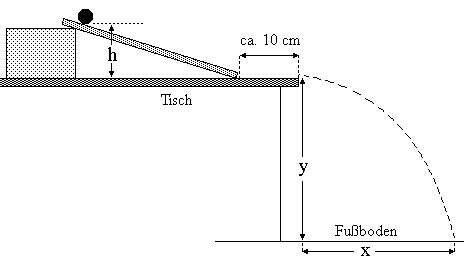
Erläutere, warum der nebenstehend gezeichnete einfache Versuch, bei dem eine Kugel eine schiefe Ebene hinunter rollt, nicht zum Rasierklingenversuch gleichwertig ist.

