In der folgenden Animation siehst du einen Körper, der in der Luft ruht. Du kannst links oben die Form des Körpers auswählen. Das schwarze Kreuz innerhalb des Körpers markiert seinen Schwerpunkt.
Kräfte und Größen in der Simulation
Wenn du die Animation mit dem Knopf unten startest, so bewegt sich der Körper mit konstanter Geschwindigkeit \(\vec v\) nach rechts durch die Luft. Den Betrag \(v\) der Geschwindigkeit kannst du mit dem Schieberegler in gewissen Grenzen verändern. Im gleichen Augenblick erscheint die sogenannte Luftwiderstandskraft \(\vec F_{\rm{LR}}\), die entgegen der Bewegungsrichtung wirkt. Der Betrag \(F_{\rm{LR}}\) der Luftwiderstandskraft wird links angezeigt.
Damit der Klotz nicht durch die Luftwiderstandskraft abgebremst wird, sondern mit konstanter Geschwindigkeit weitergleitet, ist eine Zugkraft \(\vec F_{\rm{Z}}\) notwendig. Diese Zugkraft muss in Bewegungsrichtung gerichtet sein und den gleichen Betrag wie die Luftwiderstandskraft haben. In der Animation wird die Zugkraft automatisch der Luftwiderstandskraft angepasst.
Zusammenhänge zwischen den Größen
In der Animation kannst du erkennen, dass sich der Betrag \(F_{\rm{LR}}\) der Luftwiderstandskraft ändert, wenn du den Betrag \(v\) der Geschwindigkeit oder die Form des Körpers änderst. Wenn du auf die kleine Checkbox links klickst, wird dir die Auswertung und das Ergebnis der Experimente zum Luftwiderstand angezeigt.
Eigenschaften der Luftwiderstandskraft und Definition des \(c_{\rm{w}}\)-Wertes
Wenn
- sich ein Körper relativ zur Luft bewegt
dann wirkt auf diesen Körper eine Kraft, die sogenannte Luftwiderstandskraft \(\vec F_{\rm{LR}}\). Es gilt:
- Die Luftwiderstandskraft \(\vec F_{\rm{LR}}\) wirkt immer entgegen der Bewegungsrichtung des Körpers.
- Der Betrag \(F_{\rm{LR}}\) der Luftwiderstandskraft verändert sich in Abhängigkeit vom Betrag \(v\) der Geschwindigkeit und der Form des Körpers. Der Betrag der Luftwiderstandskraft ist weiter - was in der Animation nicht dargestellt wird - abhängig von der Querschnittsfläche \(A\), die der Körper der Luft entgegenstellt und schließlich der Dichte \(\rho_{\rm{Luft}}\) der Luft.
Die Auswertung der entsprechender Experimente ergibt:
- Der Betrag \(F_{\rm{LR}}\) der Luftwiderstandskraft ist proportional zum Quadrat des Betrags \(v\) der Geschwindigkeit, zur Querschnittsfläche \(A\) und zur Dichte \(\rho_{\rm{Luft}}\) der Luft.
- Die Proportionalitätskonstante, die man mit dem Buchstaben \(c_{\rm{w}}\) (sprich "c-w") bezeichnet und Luftwiderstandsbeiwert nennt, hängt von der Form des Körpers ab.
- Schließlich beinhaltet die Formel noch den Faktor \(\frac{1}{2}\); seine Herkunft beruht auf theoretischen Überlegungen, die wir weiter unten kurz vorstellen.
Kurz
\[\color{Red}{F_{\rm{LR}}} = \frac{1}{2} \cdot A \cdot c_{\rm{w}} \cdot \rho_{\rm{Luft}} \cdot \color{Blue}{v}^2 \quad(1)\]
mit dem von der Form des Körpers Luftwiderstandsbeiwert \(c_{\rm{w}}\). Der Luftwiderstandsbeiwert hat keine Maßeinheit, man sagt er ist "dimensionslos". Die Luftwiderstandsbeiwerte für verschiedene Formen von Körpern findest du z.B. bei Wikipedia.
Mathematische Herleitung (für Interessierte)
Im Folgenden soll anhand eines einfachen Modells eines Radfahrers gezeigt werden, wie man mit einer energetischen Überlegung auf die Formel \((1)\) kommt.
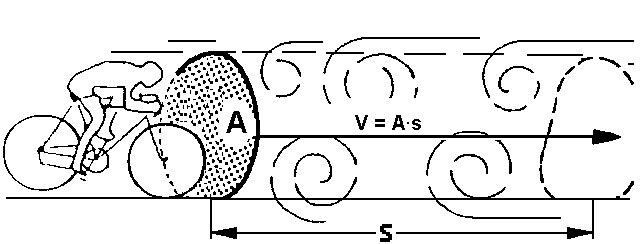
Der Radfahrer in der Abbildung muss eine Kraft aufbringen, um die vor ihm liegende Luft um eine Strecke \(s\) wegzuschieben. Diese Kraft ist genau so groß wie die Luftwiderstandskraft \(\vec F_{\rm{LR}}\). Dabei verrichtet der Radfahrer an der Luft Beschleunigungsarbeit. Der Betrag dieser Beschleunigungsarbeit ist\[{W_{\rm{Beschleunigung}}} = F_{\rm{LR}} \cdot s \quad(*)\]Die Luft erhält dabei die kinetische Energie \[{E_{\rm{kin}}} = \frac{1}{2} \cdot {m_{\rm{Luft}}} \cdot {v_{\rm{Luft}}}^2\]Ersetzt man die Masse der Luft durch das Produkt aus Volumen (\(V = A \cdot s\)) und Dichte \(\rho_{\rm{Luft}}\), so gilt \({m_{\rm{Luft}}} = \rho_{\rm{Luft}} \cdot A \cdot s\) und somit\[{E_{\rm{kin}}} = \frac{1}{2} \cdot \rho_{\rm{Luft}} \cdot A \cdot s \cdot {v_{\rm{Luft}}}^2 \quad(**)\] \({v_{\rm{Luft}}}\) ist die der Luft erteilte Geschwindigkeit. Sie ist nur bei einer Kreisscheibe, welche die Luft wegschiebt, gleich der Geschwindigkeit \(v\) des bewegten Körpers. Je nach der Form des Körpers unterscheidet sich \({v_{\rm{Luft}}}\) von \(v\), jedoch gilt annähernd \({v_{\rm{Luft}}} \sim v\). Man setzt \({v_{\rm{Luft}}}^2 = {c_{\rm{w}}} \cdot {v^2}\) und erhält durch Ersetzen von \(v_{\rm{Luft}}\) in \((**)\) und Gleichsetzen von \((*)\) und \((**)\) und die gesuchte Formel für den Luftwiderstand:
\[\begin{eqnarray}{W_{{\rm{Beschleunigung}}}} &=& {E_{{\rm{kin}}}}\\{F_{{\rm{LR}}}} \cdot s &=& \frac{1}{2} \cdot {\rho _{{\rm{Luft}}}} \cdot A \cdot s \cdot {c_{\rm{w}}} \cdot v^2 \quad \left| {:s} \right.\\{F_{{\rm{LR}}}} &=& \frac{1}{2} \cdot {\rho _{{\rm{Luft}}}} \cdot A \cdot {c_{\rm{w}}} \cdot v^2\end{eqnarray}\]
Mathematische Hilfen
Um Aufgaben zur Luftreibung zu lösen musst du häufig die Gleichung \({F_{\rm{LR}}} = {\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2\) nach einer Größe, die unbekannt ist, auflösen. Wie du das machen kannst zeigen wir dir in der folgenden Animation.
Vertausche die beiden Seiten der Gleichung.
\[{\frac{1}{2}} \cdot {\color{Red}{A}} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2 = {F_{\rm{LR}}}\]
\[\frac{{{\frac{1}{2}} \cdot {\color{Red}{A}} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2}}{{\frac{1}{2}} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2} = \frac{{F_{\rm{LR}}}}{{\frac{1}{2}} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2}\]
Vertausche die beiden Seiten der Gleichung.
\[{\frac{1}{2}} \cdot {A} \cdot {\color{Red}{c_{\rm{W}}}} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2 = {F_{\rm{LR}}}\]
\[\frac{{{\frac{1}{2}} \cdot {A} \cdot {\color{Red}{c_{\rm{W}}}} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2}}{{\frac{1}{2}} \cdot {A} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2} = \frac{{F_{\rm{LR}}}}{{\frac{1}{2}} \cdot {A} \cdot {\rho_{\rm{Luft}}} \cdot {v}^2}\]
Vertausche die beiden Seiten der Gleichung.
\[{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {\color{Red}{\rho_{\rm{Luft}}}} \cdot {v}^2 = {F_{\rm{LR}}}\]
\[\frac{{{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {\color{Red}{\rho_{\rm{Luft}}}} \cdot {v}^2}}{{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {v}^2} = \frac{{F_{\rm{LR}}}}{{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {v}^2}\]
Vertausche die beiden Seiten der Gleichung.
\[{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}} \cdot {\color{Red}{v}}^2 = {F_{\rm{LR}}}\]
\[\frac{{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}} \cdot {\color{Red}{v}}^2}{{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}}} = \frac{{F_{\rm{LR}}}}{{\frac{1}{2}} \cdot {A} \cdot {c_{\rm{W}}} \cdot {\rho_{\rm{Luft}}}}\]

