Fahrradfahren kostet Kraft - selbst dann - wenn man sich auf ebener Strecke mit konstanter Geschwindigkeit fortbewegen will. Auf den ersten Blick könnte man meinen, dass dies ein Widerspruch zum Trägheitssatz von Newton ist, doch bei näherer Betrachtung stellt man fest, dass es beim Radfahren eine Reihe von Kräften gibt, die es zu überwinden gilt. Neben der gleichförmigen Fahrt in der Ebene soll im Folgenden auch kurz auf die Bergfahrt und auf den Beschleunigungsvorgang (Geschwindigkeitszunahme) eingegangen werden.
Rollreibungskraft (Rollwiderstand)
Die Rollreibungskraft \(F_{\rm{RR}}\), oft auch Rollwiderstand genannt, kommt dadurch zustande, dass der Reifen beim Abrollen auf der Unterlage dauernd verformt werden muss.
Näherungsweise lässt sich der Rollwiderstand mit folgender Beziehung berechnen:
Rollreibungskraft
Für die Rollreibungskraft \(F_{\rm{RR}}\) gilt:\[F_{\rm{RR}}=\mu_{\rm{RR}}\cdot F_{\rm{N}}\]Dabei ist \(\mu_{\rm{RR}}\) der Rollreibungskoeffizient und \(F_{\rm{N}}\) der Betrag der Normalkraft.
Die Rollreibungskraft \(F_{\rm{RR}}\) ist dabei entgegengesetzt zur Bewegungsrichtung gerichtet.
Der Rollreibungskoeffizient \(\mu_{\rm{RR}}\) ist dabei weitgehend unabhängig von der Geschwindigkeit. Mit zunehmendem Raddurchmesser sinkt jedoch die Rollreibungskraft, große Räder rollen leichter als kleine Räder.
Luftdruck beeinfluss die Rollreibungskraft
Ein wesentlicher Einflussfaktor für die Rollwiderstand ist die Größe des Luftdrucks im Reifen: (Daten aus der Sendung Quark & Co. des WDR über das Fahrrad)
| Reifentyp | Breite \(b\) | Durchmesser \(d\) | Rollreibungskoeffizient \(\mu_{\rm{RR}}\) | ||
|---|---|---|---|---|---|
| \(p=3\,\rm{bar}\) | \(p=4\,\rm{bar}\) | \(p=5\,\rm{bar}\) | |||
| Slik-Reifen, breit | 32mm | 622mm | 0,00513 | 0,00361 | - - - |
| Slik-Reifen, mittel | 28mm | 622mm | 0,00596 | 0,00404 | 0,00349 |
| Slik-Reifen, schmal | 20mm | 622mm | - - - | 0,00477 | 0,00376 |
| Profilreifen | 37mm | 622mm | 0,00545 | 0,00404 | - - - |
| Tour de Sol-Reifen | 47mm | 305mm | 0,00669 | 0,00436 | 0,00378 |
Aufgaben
Aufgabe
Studiere obige Tabelle und formuliere sogenannte "Je-desto-Beziehungen" zwischen
- \(\mu_{\rm{RR}}\) und Druck \(p\) bei festem \(d\) und \(b\).
- \(\mu_{\rm{RR}}\) und Reifenbreite \(b\) bei festem \(d\) und \(p\).
-
\(\mu_{\rm{RR}}\) und Reifendurchmesser \(d\) bei festem \(p\) und \(b\).
Erläutere physikalisch, warum in einigen Zellen der Tabelle nur Striche sind.
Eine Druckerhöhung bringt eine geringeren Rollreibungskoeffizient \(\mu_{\rm{RR}}\). Erläutere, mit welchem Nachteil man sich diesen Vorteil erkauft.
Fahrbahn beeinfluss den Rollreibungskoeffizienten
Der Rollreibungskoeffizient \(\mu_{\rm{RR}}\) hängt stark von der Bodenbeschaffenheit ab. Die obigen Werte für die Rollreibungskoeffizienten (die für glatte Fahrbahnen gelten) sind bei anderen Fahrbahnen mit folgenden Faktoren zu multiplizieren:
| Bodenbeschaffenheit | Faktor |
|---|---|
| Glatte Fahrbahn | \(1{,}0\) |
| Kopfsteinpflaster | \(1{,}5\) |
| fest gefahrener Sand | \(4{,}0\) |
Beispiel
Reibungswiderstand
Die Reibungswiderstandskraft \(F_{\rm{R}}\) wird durch die Reibung in den Lagern und in der Kette verursacht. Im Vergleich zur Rollreibungskraft \(F_{\rm{RR}}\) spielt sie keine so große Rolle, da sie deutlich geringer ist.
Bei unserem Musterradler Richard, dessen Masse mit Rad \(m = 90\,\rm{kg}\) ist, beträgt die Reibungswiderstandskraft \(F_{\rm{R}}\) nur rund \(F_{\rm{R}}=0{,}20\,\rm{N}\).
Radwiderstand
Die Radwiderstandskraft \(F_{\rm{Rad}}\) ist die Summe aus dem Reibungswiderstand \(F_{\rm{R}}\) und der Rollreibungskraft \(F_{\rm{RR}}\):\[F_{\rm{Rad}}=F_{\rm{R}}+F_{\rm{RR}}\]Unser Musterradler Richard, der zusammen mit seinem Fahrrad eine Masse von \(m=90\,\rm{kg}\) besitzt, hat also einen Radwiderstand von:\[F_{\rm{Rad}}=0{,}2\,\rm{N}+3{,}8\,\rm{N}=4{,}0\,\rm{N}\]
Luftwiderstand
Wie Du aus der Erfahrung sicher weißt, nimmt die Luftwiderstandskraft FL mit der Geschwindigkeit v zu. Wie groß sie ist, hängt aber auch davon ab, wie "windschlüpfrig" der Radfahrer samt Rad ist. Dies wird im sogenannten cw-Wert (reine Zahl) berücksichtigt. Außerdem spielt die Dichte \(\rho\) der Luft, die weg geschoben werden muss und die Stirnfläche \(A\) des Fahrers samt Rad eine Rolle.
Es gilt: \({F_L} = \frac{1}{2} \cdot {c_w} \cdot \rho \cdot A \cdot {v^2}\)
Einige Schüler werden die Herleitung dieser Formel nach dem Kapitel über die Energie verstehen können.
In der Folgenden Tabelle sind die cw-Werte und die Stirnflächen für verschiedene Fahrradtypen zusammengestellt.
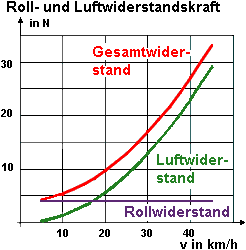
Die folgende Graphik zeigt recht eindrucksvoll, wie die Luftwiderstandskraft \(F_{\rm{L}}\) mit der Geschwindigkeit \(v\) zunimmt. In diese Zeichnung ist auch noch die Radwiderstandskraft unseres Musterradlers Richard von \(F_{\rm{Rad}}=4\,\rm{N}\) eingetragen.
Fährt unser Radler in der Ebene mit konstanter Geschwindigkeit (d.h. Beschleunigungswiderstand und Steigungswiderstand sind Null), so gilt:
\[\rm{Gesamtwiderstand = Radwiderstand + Luftwiderstand}\]
Die Abhängigkeit der Gesamtwiderstandskraft von der Geschwindigkeit ist rot markiert. Man sieht aus der Grafik, dass schon ab einer Geschwindigkeit von ca. 18 km/h der Luftwiderstand größer ist als der Radwiderstand.
Zu hohen Geschwindigkeiten hin - wie sie bei Radrennen gefahren werden - dominiert der Luftwiderstand. Es ist daher verständlich, dass die Fahrer versuchen im Windschatten der Konkurrenten zunächst Kraft zu sparen.
Aufgabe
Aufgabe
Ermittle mit Hilfe der Grafik, bei welcher Geschwindigkeit \(v\) der Luftwiderstand viermal so hoch ist wie der Radwiderstand, der bei unserem Musterradler Richard \(4{,}0\,\rm{N}\) beträgt.