Harmonische Schwingungen und Trigonometrische Funktionen
Harmonische Schwingungen können durch die Trigonometrischen Funktionen "Sinus" und "Cosinus" beschrieben werden. Welche der beiden Funktionen man am besten benutzt hängt von der Anfangssituation der Schwingung ab:
- Hat die Schwingung zur Zeit \(t = 0\) die Auslenkung (Elongation) \(y(0)=0\), benutzt man wegen \(\sin(0)=0\) besser die Sinusfunktion.
- Hat die Schwingung dagegen zur Zeit \(t = 0\) eine bestimmte Auslenkung (Elongation) \(y(0)=y_0 \ne 0\), benutzt man wegen \(\cos(0)=1\) besser die Cosinusfunktion. Da in der Schule dieser zweite Fall viel häufiger auftritt benutzen wir in unseren Ausführungen meistens die Cosinusfunktion.
Will man eine harmonische Schwingung ganz allgemein beschreiben, so wählt man die Funktion \(y(t) = \hat y \cdot \cos \left( {\omega \cdot t + \varphi_0 } \right)\) oder \(y(t) = \hat y \cdot \sin \left( {\omega \cdot t + \varphi_0 } \right)\). Dabei gelten folgende Bezeichnungen:
- \(\hat y\): Amplitude (maximale Auslenkung); \(\left[ {\hat y} \right] = 1\,\rm{m}\)
- \(\omega \): Kreisfrequenz; \(\left[ \omega \right] = \frac{1}{\rm{s}}\)
- \(\varphi_0 \): Phasenverschiebung; \(\left[ \varphi_0 \right] = 1\)
Weiter gelten die bekannten Bezeichnungen
- \(T\): Schwingungsdauer; \(\left[ T \right] = 1\,{\rm{s}}\)
- \(f\): Frequenz; \(\left[ f \right] = \frac{1}{\rm{s}} = 1\,{\rm{Hz}}\)
und die Zusammenhänge\[f = \frac{1}{T} \;\;\;{\rm{und}}\;\;\;\omega = 2\,\pi \cdot f = \frac{2\,\pi}{T}\]
Im Weiteren zeigen wir dir, wie du den Term bzw. den Graphen der allgemeinen Funktion \(y(t) = \hat y \cdot \cos \left( {\omega \cdot t + \varphi_0 } \right)\) oder \(y(t) = \hat y \cdot \sin \left( {\omega \cdot t + \varphi_0 } \right)\) so verändern kannst, dass er eine konkrete harmonische Schwingung mit bekannter Amplitude, Schwingungsdauer (und evtl. Phasenverschiebung) beschreibt.
Prinzipiell musst du zuerst einmal entscheiden, ob du die Sinusfunktion oder die Cosinusfunktion nutzen willst:
- Hat die Schwingung zur Zeit \(t = 0\) die Auslenkung (Elongation) \(y(0)=0\), benutzt man wegen \(\sin(0)=0\) besser die Sinusfunktion.
- Hat die Schwingung dagegen zur Zeit \(t = 0\) eine bestimmte Auslenkung (Elongation) \(y(0)=y_0 \ne 0\), benutzt man wegen \(\cos(0)=1\) besser die Cosinusfunktion.
Da in der Schule dieser zweite Fall viel häufiger auftritt benutzen wir in unseren Ausführungen meistens die Cosinusfunktion.
Anpassung an die Amplitude
Hat die konkrete harmonische Schwingung die Amplitude \(\hat y\), dann musst du diesen Wert in die allgemeine Funktion einsetzen. Der Graph der Funktion wird dadurch in \(y\)-Richtung gestreckt bzw. gestaucht.
Anpassung an die Kreisfrequenz
Hat die konkrete harmonische Schwingung die Schwingungsdauer \(T\) und damit die Kreisfrequenz \(\omega = \frac{2\,\pi}{T}\), dann musst du diesen Wert in die allgemeine Funktion einsetzen. Der Graph der Funktion wird dadurch in \(t\)-Richtung gestreckt bzw. gestaucht.
Anpassung an eine eventuelle Phasenverschiebung
Ist die konkrete harmonische Schwingung zeitlich gegen eine andere Schwingung verschoben, dann sprechen wir von einer Phasenverschiebung \(\varphi_0\) dieser Schwingung (gegen die andere).
Bei einer zeitlichen Verschiebung um eine Zeitspanne \(\Delta t\) berechnet sich die Phasenverschiebung zu \(\varphi_0 = \omega \cdot \Delta t\).
Diesen Wert musst du in die allgemeine Funktion einsetzen. Der Graph der Funktion wird dadurch in \(t\)-Richtung nach rechts (\(\varphi_0 < 0\)) oder links (\(\varphi_0 > 0\)) verschoben.
Hinweis: Die obige Animation zeigt auch, dass \(\sin \left( {\omega \cdot t + \frac{1}{2}\pi } \right)\) gleich \(\cos \left( {\omega \cdot t} \right)\) ist
Anpassung an die Amplitude, die Kreisfrequenz und eine eventuelle Phasenverschiebung
Durch die Änderung der Größen \(\hat y\), \(\omega\) und \(\varphi_0\) in der allgemeinen Sinus- oder Cosinusfunktion kannst du jede beliebige harmonische Schwingung beschreiben. Der Graph der Funktion kann dabei gleichzeitig in \(y\)-Richtung gestreckt bzw. gestaucht und in \(t\)-Richtung gestreckt bzw. gestaucht und nach rechts oder links verschoben werden.
Verständnisaufgaben
Aufgabe
Skizziere den Graphen der Funktion \(y(t) = 3\, {\rm{cm}} \cdot \sin \left( {\frac{{0{,}5}}{\rm{s}} \cdot t - \frac{\pi }{2}} \right)\)
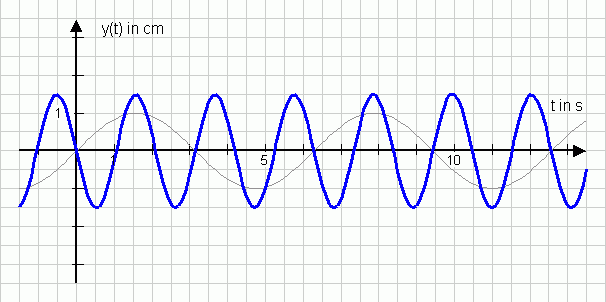
Bestimme den Funktionsterm zu folgendem Graphen.
Skizziere den Graphen der Funktion \(y(t) = 2\, {\rm{cm}} \cdot \cos \left( {\frac{2}{\rm{s}} \cdot t + \pi} \right)\)
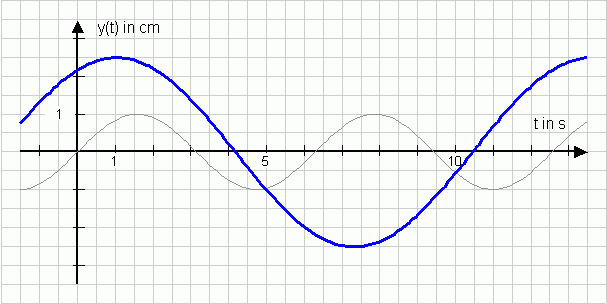
Bestimme den Funktionsterm zu folgendem Graphen.