Lineare Bewegung - Gleichungen
Aufgabe
Auswertung eines Videos mit einem fahrenden Auto
Schwierigkeitsgrad:
mittelschwere Aufgabe
Abb. 1
Aufnahme eines fahrenden Autos
Um das Video auszuwerten, muss man die Einzelbilder des Videos ausmessen. Die Einzelbilder eines Videofilms sind meist in einem Zeitabstand von 1/25 stel Sekunde aufgenommen.
In der Animation in Abb. 1 wurde jedes vierte Bild aus dem Video herausgeschnitten, so dass der Zeitabstand zwischen zwei Bildern dort 4/25stel Sekunden (= 0,16 s) beträgt.
Werte das Video mit einer Tabellenkalkulation aus und bestimme so die Geschwindigkeit des Autos.
Lösung einblendenLösung verstecken
Lösung einblendenLösung verstecken
|
Im ersten Schritt mißt man für jedes Teilbild den Abstand eines Punktes des Messobjekts (hier weisses Auto - Hinterrad) zu einem Festpunkt (hier Straßenschild) in mm. Diesen Wert x unkorrigiert trägt man in die erste Spalte des Tabellenkalkulationsprogramms ein.
|
 |
|
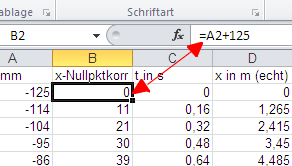
Im zweiten Schritt korrigiert man den Nullpunkt, indem man von jedem Wert den Anfangswert (-125) subtrahiert. Das Programm macht dies automatisch, wenn man ins Feld B2 eingibt:
= A2+125, und diese Eingabe in die Felder B3 bis B.. kopiert.
|
x in mm(Bild)
|
x-Nullpktkorr
|
.
|
x in m (echt)
|
|
-125
|
0
|
.
|
0
|
|
-114
|
11
|
.
|
1,265
|
|
-104
|
21
|
.
|
2,415
|
|
-95
|
30
|
.
|
3,45
|
|
-86
|
39
|
.
|
4,485
|
|
-77
|
48
|
.
|
5,52
|
|
usw
|
usw
|
,
|
usw
|
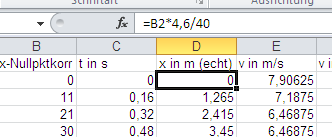
| Im dritten Schritt rechnet man aus dem Bildmaßstab ins Original um, indem man den Wert im B-Feld durch die Länge des schwarzen Autos auf dem Bild in mm (hier 40) teilt und mit der wahren Länge des Autos (hier 4,60 m) multipliziert. Dies geschieht indem man ins Feld D2 eingibt: = (B2/40)*4,60 und diese Eingabe in die Felder D3 bis D.. kopiert. |
 |
|
Im vierten Schritt ergänzt man eine Zeitskala in die Spalte C
|
x in mm(Bild)
|
x-Nullpktkorr
|
t in s
|
x in m (echt)
|
|
-125
|
0
|
0
|
0
|
|
-114
|
11
|
0,16
|
1,265
|
|
-104
|
21
|
0,32
|
2,415
|
|
-95
|
30
|
0,48
|
3,45
|
|
-86
|
39
|
0,64
|
4,485
|
|
-77
|
48
|
0,80
|
5,52
|
|
usw
|
usw
|
usw
|
usw
|
|
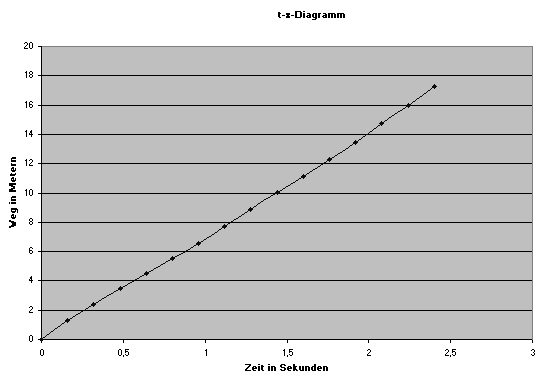
Nun kann man sich durch das Programm Excel ein t-x-Diagramm zeichnen lassen. Dazu markiert man sich die beiden Spalten (t -Spalte und x-echt-Spalte) und wählt im Menue Diagramme die Auswahl Punkte (XY) aus.
|
 |
|
Im fünften Schritt berechnet man die Momentangeschwindigkeiten, wobei diese wegen der relativ großen Meßfehler bei den x-Werten ( 1 mm Fehler bei 10 mm Wert bedeutet einen relativen Fehler von 10%) stärker schwanken als man vermutet. Dazu gibt man in das Feld E2 ein: =(D3-D2)/(C3-C2) und kopiert dies in die Felder E3 bis E..
Man kann in einer weiteren Spalte noch die Geschwindigkeit in km/h rechnen lassen.
|
x in mm(Bild)
|
x-Nullpktkorr
|
t in s
|
x in m (echt)
|
v in m/s
|
|
-125
|
0
|
0
|
0
|
7,90625
|
|
-114
|
11
|
0,16
|
1,265
|
7,1875
|
|
-104
|
21
|
0,32
|
2,415
|
6,46875
|
|
-95
|
30
|
0,48
|
3,45
|
6,46875
|
|
-86
|
39
|
0,64
|
4,485
|
6,46875
|
|
-77
|
48
|
0,80
|
5,52
|
6,46875
|
|
usw
|
usw
|
usw
|
usw
|
usw
|
|
Nun kann man sich durch das Programm Excel ein t-v-Diagramm zeichnen lassen. Dazu markiert man sich die beiden Spalten (t -Spalte und v-Spalte) und wählt im Menue Diagramme die Auswahl Punkte (XY) aus.
|

|
Grundwissen zu dieser Aufgabe
Mechanik
Lineare Bewegung - Gleichungen