Die Erde ist eine flüssige Kugel mit einer festen Kruste. Die Oberfläche dieser Flüssigkeitskugel verschiebt sich so lange, bis sie senkrecht auf den resultierenden Kräften steht. Steht die Oberfläche nicht senkrecht auf den resultierenden Kräfte, so wirkt auf die flüssigen Teile der Oberfläche eine Kraft, die diese Massepunkte verschiebt.
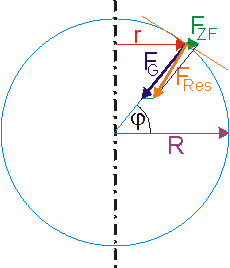
Auf alle Körper auf der Erdoberfläche wirkt die Gravitationskräfte \({\vec F_{\rm{G}}}\). Außer an Nord und Südpol wirkt eine Komponente der Gravitationskraft als Zentripetalkraft \({\vec F_{{\rm{ZP}}}}\), um die Teilchen auf der Kreisbahn zu halten. Diese Komponente der Gravitationskraft wird zum Halten der Massestücke auf der Kreisbahn verwendet und bestimmt dadurch nicht mehr die Form der Oberfläche.
Die Oberfläche der Erde steht deshalb auf dem (vektoriellen) Rest der Gravitationskraft senkrecht. Diesen Rest erhält man leichter, wenn man von der Gravitationskraft \({\vec F_{\rm{G}}}\) die Zentripetalkraft \({\vec F_{{\rm{ZP}}}}\) subtrahiert (oder alternativ wie in der Abbildung rechts dargestellt die Zentrifugalkraft \({\vec F_{{\rm{ZF}}}}\) addiert). Die resultierende Kraft \({\vec F_{{\rm{res}}}}\) dieser beiden Kräfte bestimmt die Richtung der Erdoberfläche.
Die genaue Berechnung dieser theoretischen Erdoberfläche (Erdellipsoids) ist für die 11. Klasse zu schwierig, aber eine Abschätzung der Kräfte ist möglich. Für den Drehradius \(r\) eines Orts mit der geographischen Breite \(\varphi \) gilt \(r = R \cdot \cos \left( \varphi \right)\), für den Betrag der Zentrifugalbeschleunigung \({a_{{\rm{ZF}}}}\) gilt \({a_{{\rm{ZF}}}} = r \cdot {\omega ^2}\).
Ein Zahlenbeispiel
Für \({\varphi = 45^\circ }\) gilt \(r = 6400\,{\rm{km}} \cdot \cos \left( {45^\circ } \right) = 4500\,{\rm{km}}\), daraus errechnet sich eine Zentrifugalbeschleunigung\[{a_{{\rm{ZF}}}} = 4{,}5 \cdot {10^6}\,{\rm{m}} \cdot {\left( {7{,}27 \cdot {{10}^{ - 5}}\,\frac{1}{{\rm{s}}}} \right)^2} = 0{,}024\,\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\]Daraus erkennt man, dass die Zentrifugalkraft auf der Erdoberfläche nur wenige Promille der Gravitationskraft ausmacht, der Abflachungseffekt also gering ist.
Anmerkung zur wahren Gestalt der Erde
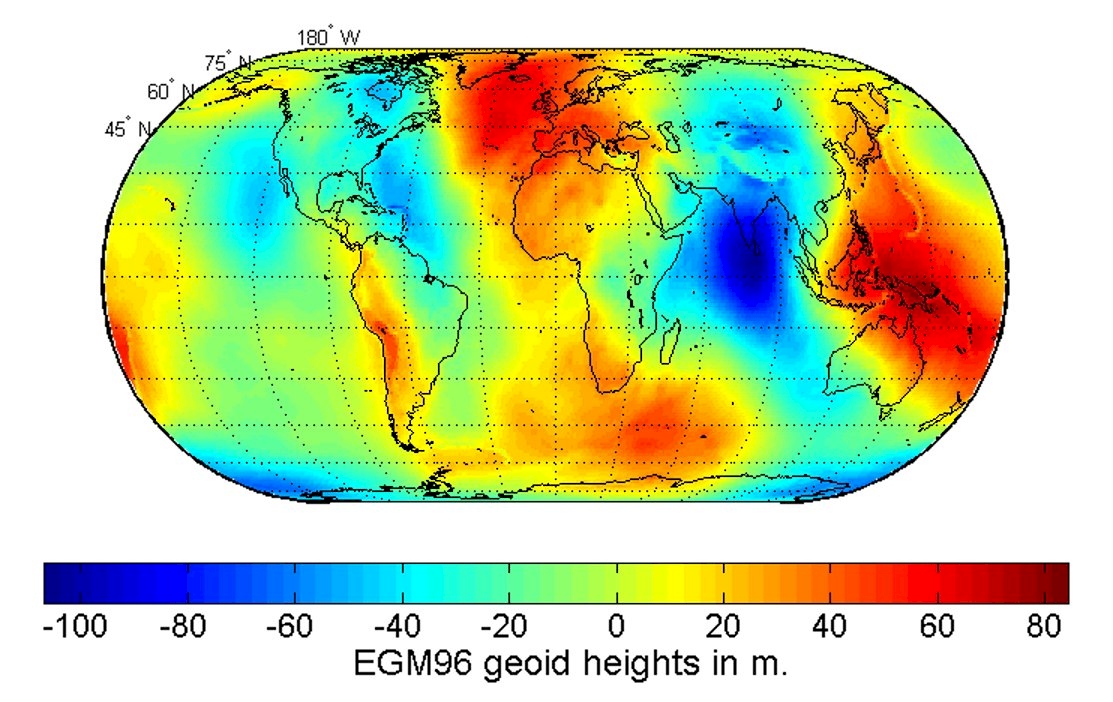
Die Geoidoberfläche wird durch die Abstände von der Referenzoberfläche des errechneten Erdelliploids definiert. Die größte negative Abweichung ist im indischen Ozean mit -106 m, die höchste Abweichung liegt bei + 85 m.