Kraft und Bewegungsänderung

Aufbau und Durchführung

Gerald Hell aus Grafenau (Links mit Sandalen im Lift) fuhr mit Personenwaage und Videokamera auf den Münchner Olympiaturm. Er filmte dabei sowohl bei der Auffahrt (Animation) vom Erdgeschoss zur Aussichtsplattform 2 als auch bei der Abfahrt die Personenwaage und wertete die Bilder aus.

Du sollst nun aus den Originaldaten mittels Tabellenkalkulation die Höhe der Liftfahrt bestimmen. Unten findest du dazu die Originaldaten von Gerald Hell in einem Tabellenblatt. Bei den Originalvideodaten wurde jeweils jedes zweite Videobild herangezogen. Der zeitliche Abstand zweier Bilder ist demnach 2 mal eine 25stel Sekunde also \(\Delta t = 0,08\rm{s}\).

Hilfen zur Auswertung

Eine Personenwaage misst im Ruhefall die Gewichtskraft der Person, gibt aber auf der Skala deren Masse an, wobei der Ortsfaktor \(g = 9,81\frac{{\rm{N}}}{{{\rm{kg}}}}\) vorausgesetzt wird.

Fährt eine auf einer Personenwaage stehende Person auf den Münchner Olympiaturm so zeigt diese während der Anfahr- und Abbremsphase nicht das tatsächliche Gewicht (bzw. die tatsächliche Masse) der Person an, sondern einen vergrößerten bzw. verkleinerten Wert, aus dem man die Beschleunigung des Aufzugs bestimmen kann.

Kennt man außerdem noch die Zeitdauer der Anfahrphase, der Phase der Bewegung mit konstanter Geschwindigkeit und der Abbremsphase, so kann man die einzelnen Weglängen und damit die Höhe des Olympiaturms (bis zum Restaurant) bestimmen.

Kräfte auf die Waage

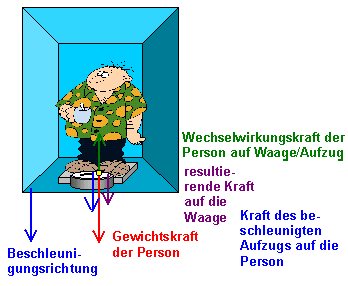
Beschleunigt der Aufzug nach oben - bei der Aufwärtsfahrt beim Anfahren, bei der Abwärtsfahrt beim Abbremsen, ergeben sich nebenstehend gezeichnete Kräfte auf die Waage, wie sie ein Außenstehender Beobachter beschreiben würde:

Die mit der Beschleunigung \(a\) bewegte Kombination Aufzug/Waage beschleunigt die Person, die als Reaktionskraft (Wechselwirkungskraft) zusätzlich zur Gewichtskraft mit \(F = m \cdot a\) auf die Waage drückt.

Der Beobachter im Lift nimmt, da er gegenüber der Kabine in Ruhe bleibt, Kräftegleichgewicht an. Trotzdem steigt die Anzeige auf der Waage und die Person kommt sich auch schwerer vor (Drückendes Gefühl im Magen). Er folgert deshalb auf eine zusätzliche nach unten wirkende Kraft, die er als Trägheitskraft erkennt, da er von der Beschleunigung des Lifts weiß. Aus der Trägheitskraft nach unten folgt eine Beschleunigung des Systems nach oben.

Beschleunigt der Aufzug nach unten - bei der Aufwärtsfahrt beim Abbremsen, bei der Abwärtsfahrt beim Anfahren - ergeben sich nebenstehend gezeichnete Kräfte auf die Waage, wie sie ein Außenstehender Beobachter beschreiben würde:

Die mit der Beschleunigung \(a\) bewegte Kombination Aufzug/Waage beschleunigt die Person nach unten, die als Reaktionskraft (Wechselwirkungskraft) mit \(F = m \cdot a\) entgegen der Gewichtskraft auf die Waage drückt, die Gesamtkraft auf die Waage also verringert.

Der Beobachter im Lift erkennt ein Sinken der Anzeige auf der Waage und die Person kommt sich leichter vor. Er folgert deshalb auf eine zusätzliche nach oben wirkende Kraft, die er als Trägheitskraft erkennt, da er von der Beschleunigung des Lifts weiß. Aus der Trägheitskraft nach oben folgt eine Beschleunigung des Systems nach unten.

Beobachtungen bei der Aufwärtsfahrt

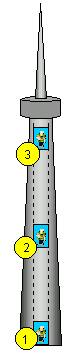
Am Anfang der Aufwärtsfahrt (1) vergrößert sich die Anzeige auf \(m' > m\). Man kann auf die resultierende Kraft \({F_{{\rm{res}}}} = m' \cdot g\) schließen. Sie setzt sich aus der tatsächlichen Gewichtskraft \({F_{\rm{G}}} = m \cdot g\) der Person und der auf sie in gleicher Richtung wirkenden Trägheitskraft \({F_{\rm{T}}} = m \cdot a\) zusammen. Es gilt somit\[{F_{{\rm{res}}}} = {F_{\rm{G}}} + {F_{\rm{T}}} \Leftrightarrow m' \cdot g = m \cdot g + m \cdot a\]und der Beschleunigungsbetrag ist\[a = \frac{{m' - m}}{m} \cdot g\]

Im Mittelteil der Fahrt (2) bewegt sich der Aufzug mit konstanter Geschwindigkeit. Hier tritt keine Änderung der Anzeige gegenüber dem Ruhezustand auf. Es ist keine Beschleunigung und damit keine Trägheitskraft vorhanden.

Am Ende der Aufwärtsfahrt (3) sinkt die Anzeige auf der Waage auf \(m' < m\). Man kann auf die resultierende Kraft \({F_{{\rm{res}}}} = m' \cdot g\) schließen. Sie setzt sich aus der tatsächlichen Gewichtskraft \({F_{\rm{G}}} = m \cdot g\) der Person und der auf sie entgegengesetzt wirkenden Trägheitskraft \({F_{\rm{T}}} = m \cdot a\) zusammen. Es gilt somit\[{F_{{\rm{res}}}} = {F_{\rm{G}}} - {F_{\rm{T}}} \Leftrightarrow m' \cdot g = m \cdot g - m \cdot a\]und der Beschleunigungsbetrag ist\[a = \frac{{m - m'}}{m} \cdot g\]

Beobachtungen bei der Abwärtsfahrt

Am Anfang der Abwärtsfahrt (1) sinkt die Anzeige auf der Waage auf \(m' < m\). Man kann auf die resultierende Kraft \({F_{{\rm{res}}}} = m' \cdot g\) schließen. Sie setzt sich aus der tatsächlichen Gewichtskraft \({F_{\rm{G}}} = m \cdot g\) der Person und der auf sie entgegengesetzt wirkenden Trägheitskraft \({F_{\rm{T}}} = m \cdot a\) zusammen. Es gilt somit\[{F_{{\rm{res}}}} = {F_{\rm{G}}} - {F_{\rm{T}}} \Leftrightarrow m' \cdot g = m \cdot g - m \cdot a\]und der Beschleunigungsbetrag ist\[a = \frac{{m - m'}}{m} \cdot g\]

Im Mittelteil der Fahrt (2) bewegt sich der Aufzug mit konstanter Geschwindigkeit. Hier tritt keine Änderung der Anzeige gegenüber dem Ruhezustand auf. Es ist keine Beschleunigung und damit keine Trägheitskraft vorhanden.

Am Ende der Abwärtsfahrt (3) vergrößert sich die Anzeige auf \(m' > m\). Man kann auf die resultierende Kraft \({F_{{\rm{res}}}} = m' \cdot g\) schließen. Sie setzt sich aus der tatsächlichen Gewichtskraft \({F_{\rm{G}}} = m \cdot g\) der Person und der auf sie in gleicher Richtung wirkenden Trägheitskraft \({F_{\rm{T}}} = m \cdot a\) zusammen. Es gilt somit\[{F_{{\rm{res}}}} = {F_{\rm{G}}} + {F_{\rm{T}}} \Leftrightarrow m' \cdot g = m \cdot g + m \cdot a\]und der Beschleunigungsbetrag ist\[a = \frac{{m' - m}}{m} \cdot g\]