Hinweis: Der folgende Versuch kann sowohl unter dem Blickwinkel der Kräfteaddition als auch der Kräftezerlegung betrachtet werden. Wenn die trigonometrischen Funktionen noch nicht bekannt sind, kann auch über die entsprechenden Längenverhältnisse am rechtwinkligen Dreieck argumentiert werden.
Versuchsaufbau
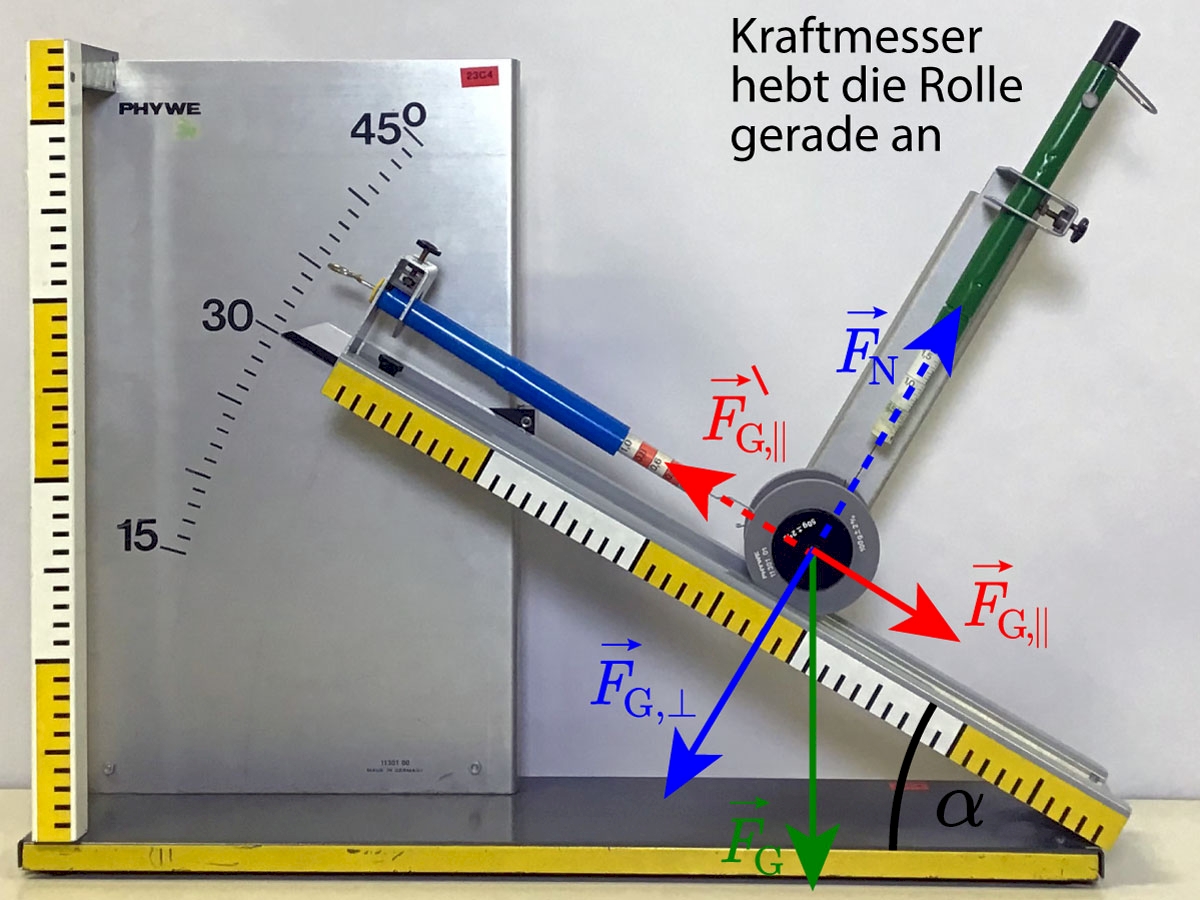
Du platzierst eine Rolle mit der Masse \(m\) auf einer schiefen Ebene mit verstellbarer Neigung. Zusätzlich montierst du in die dafür vorgesehenen Halterungen zwei Kraftmesser.
Ein Kraftmesser verläuft genau parallel zur Ebene und gleicht mit der Federkraft die parallel zur Ebene wirkende Hangabtriebskraft \(F_{\rm{G,\parallel}}\) auf. An diesem Kraftmesser kannst du also den Betrag der Hangabtriebskraft ablesen.
Der zweite Kraftmesser steht senkrecht zur Ebene und du platzierst ihn so, dass er sich in der Mitte der Rolle befindet. Weiter positionierst du den Kraftmesser so, dass der Kraftmesser die Rolle gerade von der schiefen Ebene hebt. So gleicht die Federkraft des Kraftmessers die Normalkomponente der Gewichtskraft \(F_{\rm{G,\bot }}\) gerade aus. Du kannst also an diesem Kraftmesser den Betrag der Normalkomponente der Gewichtskraft \(F_{\rm{G,\bot }}\) ablesen.
Die Federkraft entspricht somit auch der ansonsten von der Ebene aufgebrachten, nach oben gerichteten Normalkraft.
Versuchsdurchführung
Du variierst die Neigung der schiefen Ebene schrittweise und bestimmst in jeder Neigung den Betrag der parallel zur Ebene wirkenden Hangabtriebskraft\(F_{\rm{G,\parallel}}\) und den Betrag der senkrecht zur Ebene wirkenden Normalkomponente der Gewichtskraft \(F_{\rm{G,\bot }}\). Dazu musst du in jeder Einstellung den senkrecht zur Ebene stehenden Kraftmesser neu positionieren!
Die folgende Bilderserie zeigt eine entsprechende Versuchsdurchführung. Die verwendete Rolle hat dabei eine Masse von \(m=0{,}20\,\rm{kg}\). Die Gewichtskraft der Rolle beträgt daher \(F_{\rm G}=m\cdot g\approx 2{,}0\,\rm{N}\).
Beobachtung
Der Versuch liefert die folgenden Messwerte (auf eine Nachkommastelle genau abgelesen):
| Neigungswinkel \(\alpha\) der Ebene | \(15^{\circ}\) | \(20^{\circ}\) | \(25^{\circ}\) | \(30^{\circ}\) | \(35^{\circ}\) | \(40^{\circ}\) | \(45^{\circ}\) |
|---|---|---|---|---|---|---|---|
| Hangabtriebskraft \(F_{\rm{G,\parallel}}\) | 0,5 N | 0,7 N | 0,8 N | 1,0 N | 1,1 N | 1,3 N | 1,4 N |
| Normalkomponente der Gewichtskraft \(F_{\rm{G,\bot }}\) | 1,9 N | 1,9 N | 1,8 N | 1,7 N | 1,6 N | 1,5 N | 1,4 N |
Versuchsauswertung und Erklärung
Du vergleichst die gemessenen Werte mit den erwarteten Werten aus der Betrachtung im rechtwinkligen Dreieck. Entsprechend sollte für die Hangabtriebskraft \(F_{\rm{G,\parallel}}=F_{\rm{G}}\cdot \frac{h}{l}=F_{\rm{G}}\cdot \sin(\alpha)\) gelten, für die Normalkomponente der Gewichtskraft \(F_{\rm{G,\bot }}=F_{\rm{G}}\cdot \frac{b}{l}=F_{\rm{G}}\cdot \cos(\alpha)\).
| Neigungswinkel \(\alpha\) der Ebene | \(15^{\circ}\) | \(20^{\circ}\) | \(25^{\circ}\) | \(30^{\circ}\) | \(35^{\circ}\) | \(40^{\circ}\) | \(45^{\circ}\) |
|---|---|---|---|---|---|---|---|
| Hangabtriebskraft \(F_{\rm{G,\parallel}}\) | 0,5 N | 0,7 N | 0,8 N | 1,0 N | 1,1 N | 1,3 N | 1,4 N |
| \(F_{\rm{G}}\cdot \sin(\alpha)\) | 0,52 N | 0,68 N | 0,85 N | 1,0 N | 1,15 N | 1,29 N | 1,41 N |
| Normalkomponente der Gewichtskraft \(F_{\rm{G,\bot }}\) | 1,9 N | 1,9 N | 1,8 N | 1,7 N | 1,6 N | 1,5 N | 1,4 N |
| \(F_{\rm{G}}\cdot \cos(\alpha)\) | 1,93 N | 1,88 N | 1,81 N | 1,73 N | 1,64 N | 1,53 N | 1,41 N |
Die gemessenen Werte stimmen mit den erwarteten Werte überein. Die Kräftebetrachtungen mithilfe geometrischer Überlegungen am rechtwinkligen Dreieck sind somit korrekt.