Abb. 1 Impulsänderung eines sich bewegenden Wagens, auf den kurzzeitig eine Kraft wirkt
Der Impulserhaltungssatz besagt, dass in einem abgeschlossenen System der Impuls eine Erhaltungsgröße ist.
Wenn jedoch auf das abgeschlossene System von außen eine Kraft wirkt, ändert sich hierdurch der Impuls des Systems. In der Animation in Abb.1 stellt der reibungsfrei bewegliche Wagen ein abgeschlossenes System dar, was durch das rosafarbene Rechteck symbolisiert wird. Der Pendelschlag greift in dieses System ein.
Kraftstoß ändert den Impuls
Den Zusammenhang zwischen Impulsänderung \(\Delta p\) und der von außen einwirkenden Kraft \(F\) kannst du anhand des Beispiels herleiten:
Wirkt auf den Wagen während der Wechselwirkung mit dem Hammer die Kraft \(F\), so kann man nach dem newtonschen Kraftgesetz schreiben
\[F = m \cdot a\]Nimmst du vereinfachend an, dass die wirkende Kraft \(F\) bzw. die Beschleunigung \(a\) des Wagens während der Wechselwirkungsdauer \(\Delta t\) konstant ist, so gilt auch
\[F = m \cdot \frac{{\Delta v}}{{\Delta t}}\] \[\Leftrightarrow F \cdot \Delta t = m \cdot \Delta v\quad(1)\]Dabei ist \(\Delta v = {v_e} - {v_a}\), also die Änderung der Geschwindigkeit des Wagens durch den Stoß.
Das Produkt \(F\cdot \Delta t\) in Gleichung \((1)\) bezeichnet man als Kraftstoß, das Produkt \(m\cdot \Delta v\) ist die Impulsänderung \(\Delta p\). Somit folgt unter Berücksichtigung des Vektorcharakters von Kraft und Impulsänderung für den Zusammenhang von Kraftstoß und Impulsänderung:
Zusammenhang von Kraftstoß und Impulsänderung
Kraftstoß = Impulsänderung
\[\vec F \cdot \Delta t = \Delta \vec p\]
Hinweis: Obige Formel lässt sich auch in der Form \(F = \frac{{\Delta p}}{{\Delta t}}\) schreiben. Sie stellt eine Verallgemeinerung des Kraftgesetzes \(F = m \cdot a\) dar, da sie nicht nur den Zusammenhang zwischen Kraft und Geschwindigkeitsänderung, sondern auch den Zusammenhang zwischen Kraft und Massenänderung beschreibt. Dies ist dann von Interesse, wenn der beschleunigte Körper seine Masse nicht beibehält (vgl. Raketenphysik).
Anwendungen
Eine bestimmte Impulsänderung von z.B. \(100\,\rm{Ns}\) kann erreicht werden, indem man eine große Kraft \(1000\,\rm{N}\) für eine kurze Zeit von \(0{,}1\,\rm{s}\) wirken lässt. Die Impulsänderung kann aber mit einer kleineren Kraft von nur \(100\,\rm{N}\) erreicht werden. Hier muss die Kraft aber für eine längere Zeit von \(1{,}0\,\rm{s}\) wirken.
Bei einem Unfall kann der Impuls eines Autofahrers auf Null reduziert werden, indem er auf seine Windschutzscheibe "knallt". Dieser Vorgang läuft in sehr kurzer Zeit ab, die wirkende Kraft ist daher entsprechend groß.
Löst dagegen der Airbag aus, so läuft der Abbremsvorgang des Fahrers über eine längere Zeit, wodurch die wirkende Kraft entsprechend kleiner ist.
Aus diesem Grund hat man auch Kletterseile bis zu einem gewissen Grad elastisch gemacht, so dass bei einem Sturz ins Seil der Abbremsvorgang länger dauert und dadurch die Kraft auf den Gestürzten kleiner wird.
Kraft beim Stoß mit einer festen Wand
Beim Zusammenstoß eines Autos mit einer Wand könnte man vielleicht meinen, dass der links dargestellte Fall für die Insassen ungünstiger ist. Dies ist jedoch ein Trugschluss, da im linken Fall die Impulsänderung kleiner ist als im rechten Fall. Dementsprechend ist auch die Wechselwirkungskraft bei gleicher Wechselwirkungsdauer im rechten Fall größer.
Übungsaufgabe Sicherheitsgurt
Verständnisaufgabe
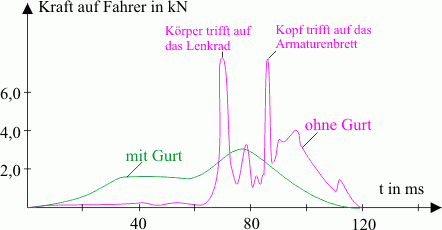
Das \(t\)-\(F\)-Diagramm in Abb. 4 zeigt den Verlauf der Kraft auf einen Autofahrer bei einem Frontalzusammenstoß, einmal mit und einmal ohne Sicherheitsgurt.
Begründe mit Hilfe der obigen Formulierung des Kraftgesetzes, wie die unterschiedlichen Verläufe zustande kommt.