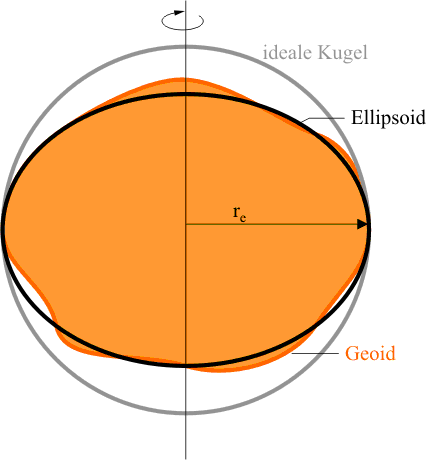
Tatsächlich kann man jedoch nicht davon ausgehen, dass die Erde eine ideale Kugel mit gleichmäßiger Massenverteilung ist. Schon aufgrund der Rotation der Erde um eine Achse, die durch den Nord- und Südpol geht, würde sich die Erde - die ja kein starrer Körper sondern in ihrem Inneren nahezu flüssig ist - zu einem Ellipsoid abplatten.
Genauere Untersuchungen haben jedoch ergeben, dass die Erde auch von der Ellipsoid-Gestalt abweicht und eine ziemlich unregelmäßige Form besitzt, die man als Geoid bezeichnet. Manche Wissenschaftler sprechen respektlos davon, dass die Erde die Form einer Kartoffel hätte.
Die Abstände von Punkten der Erdoberfläche vom Erdmittelpunkt differieren beim Geoid nicht unwesentlich, so dass schon wegen dieser Tatsache zu erwarten ist, dass die Fallbeschleunigungen auf der Geoidoberfläche verschieden ausfallen. Darüber hinaus ist die Erdkugel kein homogener Körper. Es gibt Land- und Wasserflächen, Gebirge und Lagerstätten von Erzen usw., so dass die Massenverteilung recht inhomogen ist, was wiederum eine örtlich unterschiedliche Fallbeschleunigung auf der Oberfläche bedingt.

das Grace-Duo (NASA)
Zur präzisen Ausmessung der örtlichen Fallbeschleunigungen schoss man 2002 zwei gleichartige Grace-Satelliten auf eine Erdumlaufbahn. Der Abstand der beiden Satelliten betrug ca. \(220\,\rm{km}\). Die Messung des Erdschwerefeldes erreicht man, indem die Satelliten ständig ihre eigene Position mit Hilfe eines GPS-Systems sowie zweier Sternensensoren mit hoher Genauigkeit ermitteln und darüber hinaus ihren gegenseitigen Abstand mit Hilfe von Mikrowellen bis auf Bruchteile eines Millimeters genau bestimmen. Durchfliegt z.B. der erste Satellit eine Zone erhöhter Anziehung, so wird er geringfügig stärker beschleunigt und damit erhöht sich der Abstand zum nachfolgenden Satelliten.
Fazit: Die lokalen Unterschiede in der Fallbeschleunigung bewirken eine Störung der Satellitenbahnen.
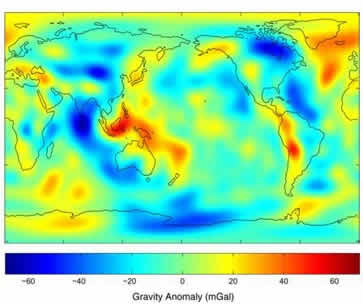
Die Auswertung der gewonnenen Daten sehen Sie in der nebenstehenden Abbildung. Sie zeigt die Abweichung der örtlichen Fallbeschleunigung von einem Standardwert. Dabei wird diese Abweichung in Milligal (\(1\,{\rm{mGal}} = {10^{-5}}\,\frac{{\rm{m}}}{{{{\rm{s}}^{\rm{2}}}}}\)) angegeben.
Man bekommt einen Eindruck von der Präzision der Messungen, wenn man sich die folgenden Angaben für die Fallbeschleunigungen am Äquator und am Pol vergegenwärtigt:\[{g_{{\rm{Pol}}}} = 983221\,{\rm{mGal}}\]\[{g_{{\rm{Äqu}}}} = 978049\,{\rm{mGal}}\]Durch die lokalen Abweichungen der Fallbeschleunigungen kann man u. U. Vorhersagen auf Öl- oder Erzvorkommen machen.
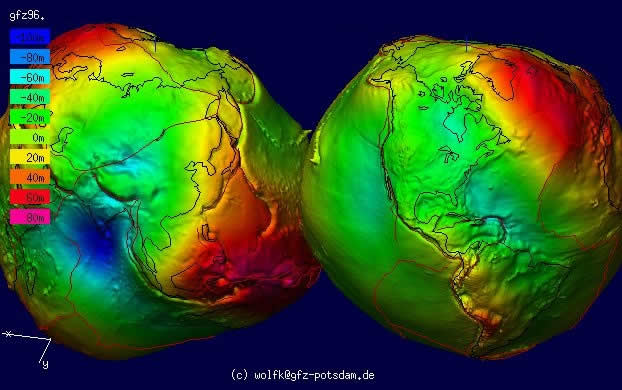
Aus den gewonnenen Werten für die lokalen Fallbeschleunigungen kann man auf die Höhen-Abweichung des Geoids vom idealen Ellipsoid schließen. Die folgenden Bilder und Animationen, welche vom Geoforschungszentrum Potsdam (GFP) stammen, geben ihnen einen Eindruck von der Unregelmäßigkeit der Erdoberfläche.
Die zwei Ansichten der Erdkugel zeigen deutlich die Abweichung von der idealen Ellipsoidgestalt. Die Erde macht den Eindruck einer Kartoffel.
Die Farbgebung der Oberfläche zeigt die jeweilige Abweichung der Oberflächenhöhe von der des Ellipsoids in Metern.
Gebiete mit roter Farbe liegen über, Gebiete mit grüner bis blauer Farbe unter der Ellipsoidoberfläche.
Unter der Adresse http://www-app2.gfz-potsdam.de/sec13/animated-potato-d-cms.html können Sie sich auch eine animierte Darstellung des Höhenprofils der Erde betrachten (Klick z.B. auf "Nordansicht").

