Zur Berechnung von Satellitenbahnen legen wir ein \(x\)-\(y\)-Koordinatensystem zugrunde, in dessen Ursprung sich das Zentralgestirn (in unserem Fall die Erde) befindet. Die Gravitationskraft wird nun in eine \(x\)- und eine \(y\)-Komponente zerlegt (siehe Abbildung). Mit diesen Kraftkomponenten werden die Bewegungen in \(x\)- bzw. \(y\)-Richtung unabhängig voneinander untersucht. Die Bahnkurve erhält man durch Zusammenführung der Ergebnisse in einem \(x\)-\(y\)-Diagramm.

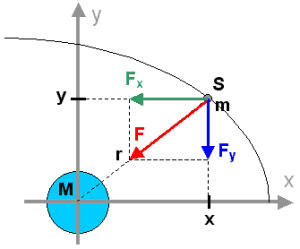
Nach dem Strahlensatz mit S als Zentrum und dem Satz des PYTHAGORAS gilt
\[\frac{{{F_x}}}{x} = - \frac{F}{r}\;{\rm{und}}\;\frac{{{F_y}}}{y} = - \frac{F}{r}\;{\rm{mit}}\;r = \sqrt {{x^2} + {y^2}} \]
Mit dem Gravitationsgesetz und dem 2. NEWTONschen Gesetz folgt für die \(x\)- bzw. \(y\)-Komponente der Beschleunigung
\[\left. \begin{array}{l}{F_x} = - \frac{F}{r} \cdot x\\{F_y} = - \frac{F}{r} \cdot y\\F = G \cdot \frac{{m \cdot M}}{{{r^2}}}\end{array} \right\} \Rightarrow \begin{array}{*{20}{c}}{{F_x} = - G \cdot \frac{{m \cdot M}}{{{r^3}}} \cdot x \Rightarrow {a_x} = \frac{{{F_x}}}{m} = - G \cdot \frac{M}{{{r^3}}} \cdot x}\\{{F_y} = - G \cdot \frac{{m \cdot M}}{{{r^3}}} \cdot y \Rightarrow {a_y} = \frac{{{F_y}}}{m} = - G \cdot \frac{M}{{{r^3}}} \cdot y}\end{array}\]
Bei der iterativen Berechnung der Satellitenbahnen soll das Halbschrittverfahren angewandt werden. Eine allgemeine Erläuterung dieses Verfahrens findet man im Beitrag "Kleine Schritte" des Kapitels "Lineare Bewegung". Mit den Vorüberlegungen von oben ergibt sich nun folgende Iterationsvorschrift:
\[(1)\quad {a_x}(t) = - G \cdot \frac{M}{{{r^3}}} \cdot x(t)\;;\;{a_y}(t) = - G \cdot \frac{M}{{{r^3}}} \cdot y(t)\;{\rm{mit}}\;r = \sqrt {x{{(t)}^2} + y{{(t)}^2}} \]
\[(2)\quad {v_x}(t + \frac{{\Delta t}}{2}) = {v_x}(t - \frac{{\Delta t}}{2}) + {a_x}(t) \cdot \Delta t\;;\;{v_y}(t + \frac{{\Delta t}}{2}) = {v_y}(t - \frac{{\Delta t}}{2}) + {a_y}(t) \cdot \Delta t\]
\[(3)\quad x(t + \Delta t) = x(t) + {v_x}(t + \frac{{\Delta t}}{2}) \cdot \Delta t\;;\;y(t + \Delta t) = y(t) + {v_y}(t + \frac{{\Delta t}}{2}) \cdot \Delta t\]
Für die Startwerte setzen wir zunächst einmal \(x(0) = 7500({\rm{km}})\), \(y(0) = 0({\rm{km}})\), \({v_x}(0) = 0(\frac{{{\rm{km}}}}{{\rm{s}}})\), \({v_y}(0) = 9(\frac{{{\rm{km}}}}{{\rm{s}}})\) und \(\Delta t = 60(\rm{s})\). Beim 1. Schritt des Verfahrens weicht die Iterationsvorschrift für die Geschwindigkeit von der allgemeinen Iterationsvorschrift \((2)\) ab:
\[(2^*)\quad {v_x}(\frac{{\Delta t}}{2}) = {v_x}(0) + {a_x}(t) \cdot \frac{{\Delta t}}{2}\;;\;{v_y}(\frac{{\Delta t}}{2}) = {v_y}(0) + {a_y}(t) \cdot \frac{{\Delta t}}{2}\]
Diese Iteration soll nun in eine Tabellenkalkulation z.B. EXCEL oder Calc übertragen werden:
1. Schritt: Gib Deinem EXCEL-Blatt einen Titel (z.B. mit Hilfe eines Textfeldes).
2. Schritt: Weise den Startwerten beschriftete Eingabezellen zu und benenne diese Zellen in geeigneter Weise um, z.B.
| Startwert | G.M | x(0) | y(0) | vx0 | vy0 | \(\Delta t\) |
| Name der Zelle | c | x0 | y0 | vx0 | vy0 | dt |
Der erste Abschnitt des EXCEL-Blattes könnte dann so aussehen:
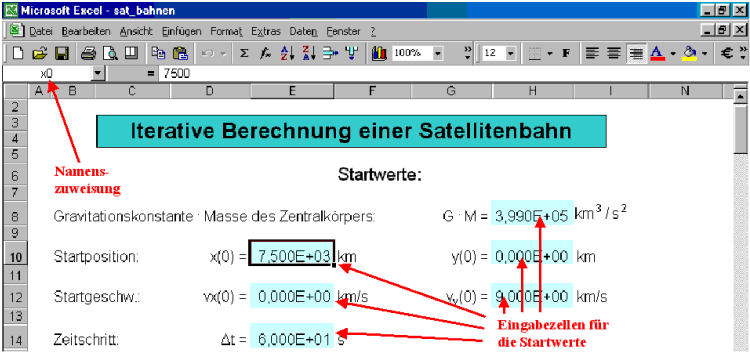
3. Schritt: Erstelle die Iterationstabelle nach folgendem Muster:
| A | B | C | D | E | F | G | H | |
| 1 | ||||||||
| ... | ||||||||
| 16 | t | x(t) | y(t) | r(t) | ax(t) | ay(t) | vx(t+dt/2) | vy(t+dt/2) |
| 17 | 0 | =x0 | =y0 | =WURZEL((POTENZ(C17;2)+POTENZ(D17;2))) | =-c*C17/ POTENZ(E17;3) |
=-c*D17/ POTENZ(E17;3) |
=vx0+(dt/2)*F17 | =vy0+(dt/2)*G17 |
| 18 | =B17+dt | =C17+dt*H17 | =D17+dt*I17 | =WURZEL((POTENZ(C18;2)+POTENZ(D18;2))) | =-c*C18/ POTENZ(E18;3) |
=-c*D18/ POTENZ(E18;3) |
=H17+dt*F18 | =I17+dt*G18 |
| 19 | =B18+dt | =C18+dt*H18 | =D18+dt*I18 | =WURZEL((POTENZ(C19;2)+POTENZ(D19;2))) | =-c*C19/ POTENZ(E19;3) |
=-c*D19/ POTENZ(E19;3) |
=H18+dt*F19 | =I18+dt*G19 |
| 20 | =B19+dt | =C19+dt*H19 | =D19+dt*I19 | =WURZEL((POTENZ(C20;2)+POTENZ(D20;2))) | =-c*C20/ POTENZ(E20;3) |
=-c*D20/ POTENZ(E20;3) |
=H19+dt*F20 | =I19+dt*G20 |
Voreinstellungen: Für alle nachfolgenden Untersuchungen sind die Werte für \(G \cdot M = {\rm{3}}{\rm{,99}} \cdot {\rm{1}}{{\rm{0}}^{\rm{5}}}\frac{{{\rm{k}}{{\rm{m}}^3}}}{{{{\rm{s}}^2}}}\) und \(R = {\rm{6}}{\rm{,368}} \cdot {10^3}{\rm{km}}\) fest.
Geben Sie folgende Startwerte ein:
| x(0) in km | y(0) in km | vx(0) in km/s | vy(0) in km/s | Δt in s |
| 7500 | 0 | 0 | 9 | 60 |
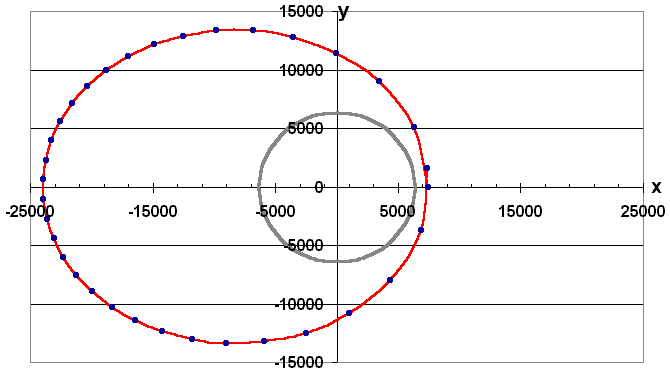
Hinweis: Die Punkte in der Grafik geben die Position des Satelliten im zeitlichen Abstand von 10·Δt an (Grund: In der Tabelle wurden jeweils 9 Zeilen ausgeblendet).
-
Wie groß ist die Umlaufdauer des Satelliten?
-
Warum haben die Punkte unterschiedliche Abstände? Was kann man daraus ablesen?
-
Bestimme aus der Grafik näherungsweise die Geschwindigkeit im erdfernsten Punkt und vergleiche diese mit der Geschwindigkeit im erdnächsten Punkt.
-
Bestimme die große Halbachse der Ellipsenbahn.
-
Überprüfe das 3. Keplersche Gesetz. Wähle hierzu den Erdmond als Vergleichskörper. (Die Bahn des Erdmondes hat eine große Halbachse von ca. 3,82.105km; seine Umlaufzeit beträgt 27,3 Tage.)
-
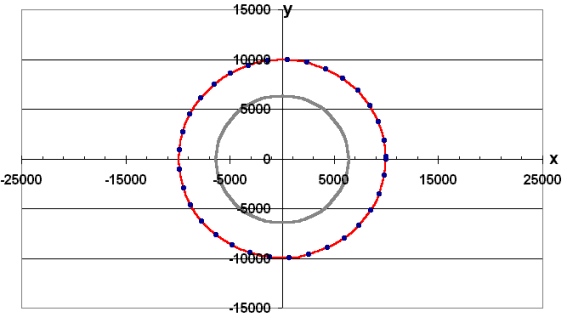
Der Startort befinde sich nun unmittelbar über der Erdoberfläche, die Geschwindigkeit sei tangential zur Erdoberfläche orientiert. Wählen Sie also z.B. für die Startwerte:
x(0) in km y(0) in km vx(0) in km/s vy(0) in km/s Δt in s 6375 0 0 15 Der Betrag der Startgeschwindigkeit ist also vy(0). Variieren Sie diesen Wert solange bis der Satellit gerade nach eine Kreisbahn um die Erde beschreibt und bestätigen Sie damit die Richtigkeit des Werts für die 1. kosmische Geschwindigkeit.
-
Der Satellit befinde sich nun 3632 km über der Erdoberfläche. Berechnen Sie die Geschwindigkeit, die erforderlich ist, dass er die Erde auf einer Kreisbahn umrundet. Überprüfen Sie diese Ergebnis mit der EXCEL-Anwendung. Wählen Sie z.B. folgende Startwerte:
x(0) in km y(0) in km vx(0) in km/s vy(0) in km/s Δt in s 10000 0 0 30 Variieren Sie vy(0) so lange, bis sich eine Kreisbahn ergibt, und vergleichen Sie die Geschwindigkeit mir dem Ergebnis von Teilaufgabe a).