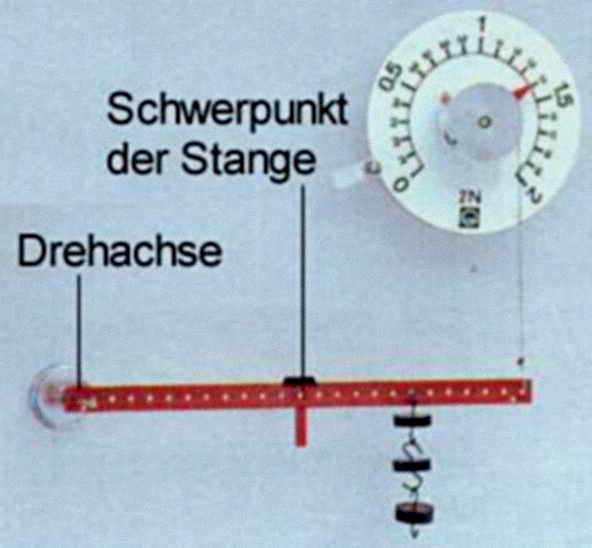
Versuch zum zweiseitigen Hebel
Abb 1 Versuch zum zweiseitigen Hebel
Aufgabe
Berechne den Betrag der Kraft \(\vec{F}_2\), die auf der rechten Seite des Hebels angreifen muss, damit sich der Hebel im Gleichgewicht befindet.
Versuch zum einseitigen Hebel
Abb 3 Versuch zum einseitigen Hebel
Aufgabe
Berechne, in welchem Abstand \(a_2\) die Kraft \(\vec{F}_2\) senkrecht zum Hebel nach oben angreifen muss, damit sich der Hebel im Gleichgewicht befindet. Nutze als Erdbeschleunigung \(g=10\,\rm{\frac{m}{s^2}}\).
Einseitiger Hebel mit mit Lagerung außerhalb des Schwerpunkts
Aufgabe
Aufgabe
Berechne den Betrag der Gewichtskraft der Hebelstange, wenn jedes Massestück die Gewichtskraft \(0{,}5\,{\rm{N}}\) hat. Die Länge der Hebelstange beträgt \(24\,{\rm{LE}}\).
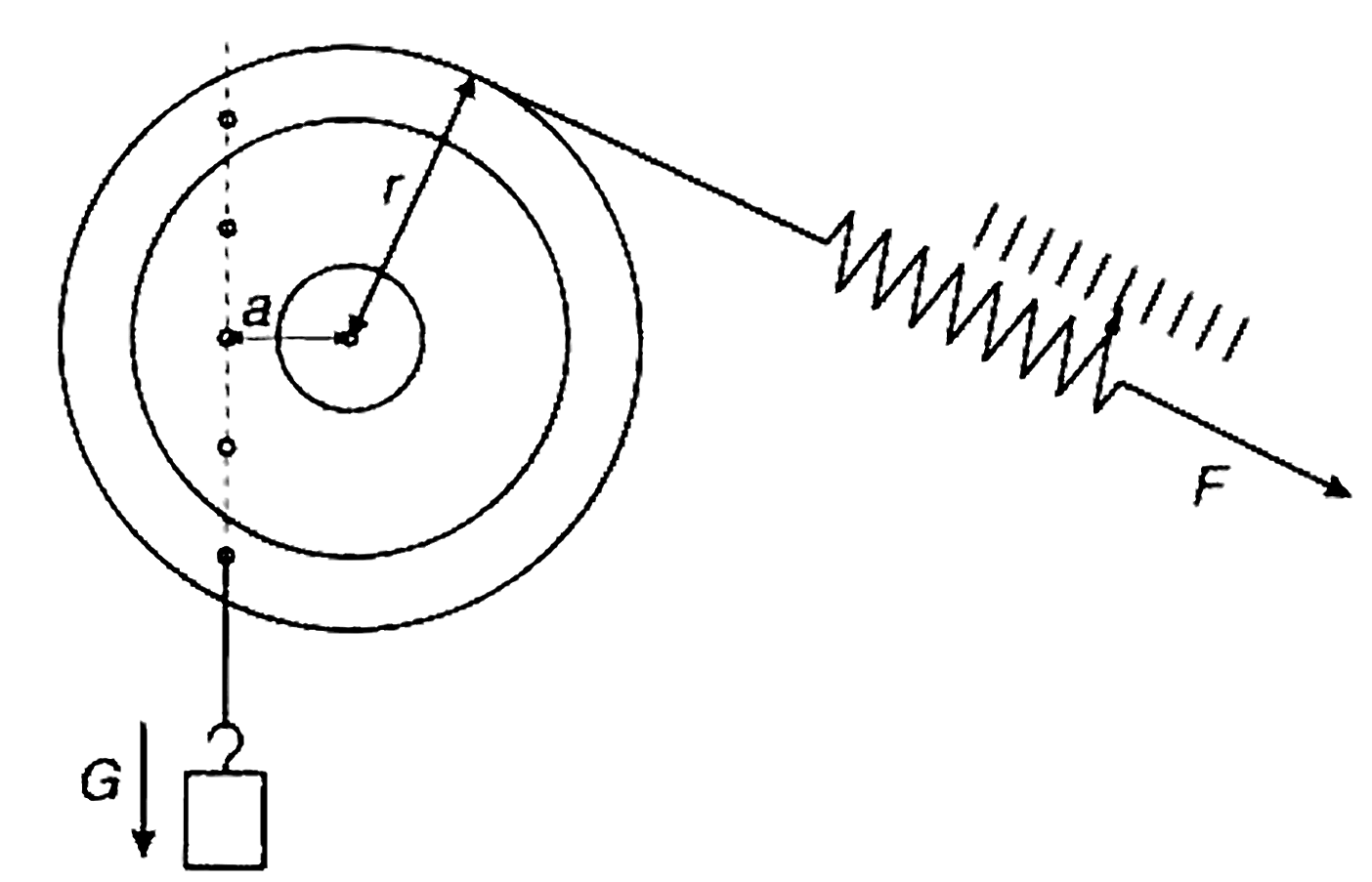
Die Drehmomentscheibe
An der Drehmomentscheibe wird deutlich, dass der Hebelarm stets das Lot auf die Wirkungslinie der Kraft ist. Egal, in welches der Löcher man das Massestück mit der Gewichtskraft \(\overrightarrow G \) einhängt, es bewirkt immer das gleiche linksdrehende Drehmoment \({M_{\rm{L}}} = G \cdot a\), was man daran erkennt, dass das zum Aufbringen des entgegenwirkenden rechtdrehenden Drehmoments \({M_{\rm{R}}}\) die Feder immer gleich weit gedehnt werden muss.