Wir haben in den Vorversuchen erkannt, dass die Spannenergie \(E_{\rm{Spann}}\) eines elastischen Körpers von seiner Federkonstante \(D\) und der Dehnung \(s\) abhängt:
- Je größer die Federkonstante des Körpers, desto größer seine Spannenergie.
- Je größer die Dehnung des Körpers, desto größer seine Spannenergie.
Um diese Abhängigkeit genauer beschreiben zu können benötigen wir eine "Formel" für die Spannenergie. Mit einigen der folgenden Versuche kannst du den Term, der diese Abhängigkeit beschreibt, durch Messreihen experimentell gewinnen. Mit anderen Versuchen kannst du die Richtigkeit des Terms bestätigen.
Wir werden jeweils am Anfang der Versuchsbeschreibung angeben, ob wir den Term gewinnen oder aber nur bestätigen wollen. Außerdem werden wir erläutern, welche Eigenschaften der Energie wir bei der Planung des Versuchs voraussetzen.
Federpendel
Ermitteln des formelmäßigen Zusammenhangs
Nun soll der genaue formelmäßige (in der Fachsprache: quantitative) Zusammenhang zwischen Spannenergie \(E_{\rm{spann}}\), Federhärte \(D\) und der Dehnung bzw. Stauchung \(s\) der Feder herausgefunden werden. Dies gelingt durch Verwendung der Formel für die potentielle Energie und des Energieerhaltungssatzes.
Du wählst dazu einen Versuch wie in Abb. 2 aus, bei dem Spannenergie möglichst reibungsfrei in potentielle Energie umgewandelt wird.
Da die Spannenergie von zwei Größen abhängt, musst du auch zwei Messreihen aufnehmen, in der du jeweils eine Größe variierst und alle anderen Größen konstant hältst.
Du dehnst eine an einer Schnur hängende Feder, deren Mitte mit einem Zeiger (rot) markiert ist, um die Strecke \(s\). Die Feder besitzt nun Spannenergie.
Lässt du die Feder los, so "springt" diese um die Höhe \(h\) nach oben. Am höchsten Punkt ist die gesamte anfängliche Spannenergie in Höhenenergie umgewandelt worden.
Formelmäßig gilt also \[E_{\text{Spann,vorher}} = E_{\text{pot,nachher}} \qquad \text{oder "salopper":} \qquad E_{Spann} = E_{pot} \qquad \text{(1)} \]
Einfluss der Dehnung \(s\)
Um den Zusammenhang zwischen der Dehnung \(s\) der Feder und \(E_{\rm{Spann}}\) zu untersuchen, nimmst du eine Messreihe auf, bei der du die Dehnung \(s\) der Feder veränderst, aber nicht die Federhärte \(D\) und die Federmesse.
Es zeigt sich, dass \[h \sim s^2\]ist. Da die Federmasse \(m\) und der Ortsfaktor \(g\) konstant waren, gilt auch:\[ m \cdot g \cdot h \sim s^2 \quad \Rightarrow \quad E_{\rm{pot}} \sim s^2 \]Mit dem Energiesatz (1) folgt:\[ \bbox[lightgreen,12px,border:2px solid grey]{E_{\rm{Spann}} \sim s^2 \qquad \text{(2)}} \]
Einfluss der Federhärte \(D\)
Nun veränderst du Federhärte \(D\) durch die Nutzung verschiedener Federn, aber dehnst diese jeweils um die gleiche Strecke \(s\). Es zeigt sich:\[ m \cdot g \cdot h \sim D \quad \Rightarrow \quad E_{pot} \sim D \]Mit dem Energiesatz (1) folgt:\[\bbox[lightgreen,12px,border:2px solid grey]{E_{\rm{Spann}} \sim D \qquad \text{(3)}}\]
Zusammenführen der Erkenntnisse
Aus (2) und (3) folgt: \[ E_{\rm{Spann}} \sim D \cdot s^2\quad\Rightarrow\quad E_{\rm{Spann}} =C\cdot D \cdot s^2 \] Eine genaue Auswertung der entsprechenden Experimente ergibt, dass der Proportionalitätsfaktor \(C\) wiederum den Wert \(\frac{1}{2}\) hat.
Rollenfahrbahn
|
Versuchsaufbau:
|
 |
|
|
Versuchsdetails:
|
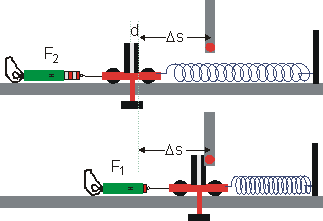 |
Versuchsergebnisse:
Abstand der Doppelunterbrecherstreifen (d = 1,0 cm); Vorspannung: F1 = 0,60 N, s1 = 20 cm; Wagenmasse: 1,00 kg
|
F1 in N
|
s1 in cm
|
Δs in cm
|
F2 in N
|
s2 in cm
|
Esp in J
|
Δt in s
|
v in m/s
|
Ekin in J
|
|
0,60
|
20
|
28,3
|
1,45
|
0,013
|
||||
|
0,60
|
20
|
20,0
|
1,20
|
0,017
|
||||
|
0,60
|
20
|
10,0
|
0,90
|
0,0265
|
Ergänze die fehlenden Spalten und überprüfe damit den Energieerhaltungssatz.