Radioaktivität - Fortführung

Versuche

ß-Spektrum

Aufbau und Durchführung

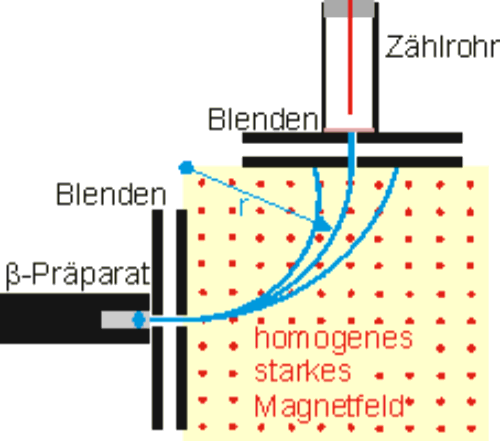
Man befestigt das abgeschirmte \(\beta\)-Präparat \(\rm{90Sr}\) vor dem rechteckigen Magnetfeld eines Elektromagneten und untersucht mit dem Zählrohr die Strahlung, die \(90°\) mit einem festen Radius \(r\) abgelenkt wird.

Abb. 2 Schematische Skizze des Versuchs.

Zur Bestimmung der Zählrate verwendet man entweder das Interface "Cassy" (siehe Foto oben ) und misst für jedes eingestellte Magnetfeld, jeweils die Zeit, bis 1000 Impulse gezählt wurden, oder man verwendet das Ratemeter und bestimmt die Zählrate mit der Mittelwertanzeige am angeschlossenen Amperemeter oder mittels einer vorgegebenen Torzeit von z.B. 100 s. (Siehe Skizze unten)

Das Magnetfeld bestimmt man am besten mit der vorher kalibrierten Hallsonde eines Teslameters.

Beobachtung

(Nulleffekt bereinigt) mit r = 35mm:

\(B \mathrm{\; in \; \frac{Vs}{m^2}}\)	0,000	0,030	0,060	0,090	0,120	0,150	0,180	0,210	0,245
\(R \mathrm{\; in \; \frac{1}{s}}\)	11,52	35,01	83,60	128,53	129,25	97,87	56,28	25,58	11,97

Auswertung

Aufgabe

Zeichne z.B. mit einer Tabellenkalkulation ein B-R-Diagramm.

Bestimme \(E_{\mathrm{kin,e}}\) in Abhängigkeit von \(B\) und zeichne ein \(E_{\mathrm{kin,e}}-R-\mathrm{Diagramm}\).

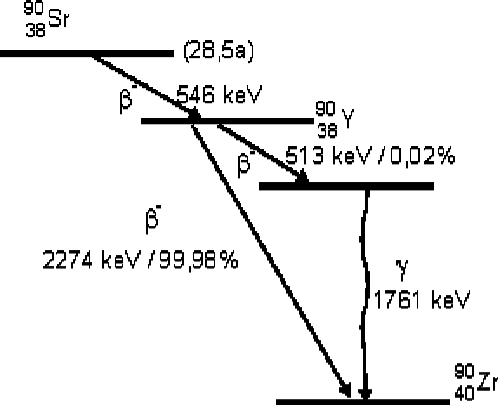
Die Theorie sagt, dass das Betaspektrum kontinuierlich ist, mit einer maximalen Energie, die dem Q-Wert des Zerfalls entspricht (siehe Termschema) und einem Maximum der Zählrate bei einem Drittel dieses Wertes. Bestimme diese Werte unter der Voraussetzung, dass nur der Sekundärzerfall von \(^{90}\rm Y\) zu sehen ist, da der Zerfall von \(^{90}\rm Sr\) nach \(^{90}\rm Y\) laut Katalogangabe durch entsprechende Abschirmung nicht zu sehen ist.

Lösung

Da die LORENTZ-Kraft als Zentripetalkraft wirkt, ergibt sich
\[\frac{{m \cdot {v^2}}}{r} = e \cdot v \cdot B \Rightarrow p = m \cdot v = e \cdot r \cdot B\]

Setzt man dies in die Energieimpulsbeziehung
\[{\left( {{E_0} + {E_{{\rm{kin}}}}} \right)^2} = {E_0}^2 + {p^2} \cdot {c^2} \Rightarrow {E_{{\rm{kin}}}} = \sqrt {{E_0}^2 + {p^2} \cdot {c^2}} - {E_0}\]

ein, so folgt

\[{E_{{\rm{kin}}}} = \sqrt {{E_0}^2 + {{\left( {e \cdot r \cdot B \cdot c} \right)}^2}} - {E_0}\]

Klammert man die Ruheenergie des Elektrons aus, so ergibt sich

\[{E_{{\rm{kin}}}} = {E_0} \cdot \left( {\sqrt {1 + \frac{{{{\left( {e \cdot r \cdot B \cdot c} \right)}^2}}}{{{E_0}^2}}} - 1} \right) = {E_0} \cdot \left( {\sqrt {1 + \frac{{{{\left( {e \cdot r \cdot B \cdot c} \right)}^2}}}{{\left( {{m_{{\rm{0}}{\rm{,e}}}} \cdot {c^2}} \right)}}} - 1} \right) = {E_0} \cdot \left( {\sqrt {1 + {{\left( {\frac{{e \cdot r \cdot B}}{{{m_{{\rm{0}}{\rm{,e}}}} \cdot c}}} \right)}^2}} - 1} \right)\]

Setzt man die Werte aus der Formelsammlung und \(r = 0,035\rm{m}\) ein, so erhält man
\[{E_{{\rm{kin}}}} = 511{\rm{keV}} \cdot \left( {\sqrt {1 + \frac{{421}}{{{{\rm{T}}^2}}} \cdot {B^2}} - 1} \right)\]

Mit Hilfe von Excel ergeben sich die folgenden Graphen, die recht gut mit der Theorie übereinstimmen: