Definition der Aktivität
Die Aktivität \(A\) eines radioaktiven Präparates dient zur Charakterisierung der "Stärke" der Strahlungsquelle. Die Aktivität \(A\) gibt dabei die Anzahl der Zerfälle \(\Delta N\) in einer radioaktiven Quelle pro Zeitintervall \(\Delta t\) an.
\[\text{Aktivität} = \frac{{{\rm{Anzahl\;der\;Zerfälle\;in\;der\;Probe}}}}{{{\rm{Messzeit}}}}\] bzw. in Kurzform\[A = \frac{{\Delta N}}{{\Delta t}}\] Die Einheit der Aktivität ist Becquerel: \(\left[A\right]=\frac{1}{1\,\rm{s}}=1\,\rm{Bq}\)
Einflussgrößen auf die Aktivität eines Präparates
- Die Aktivität \(A\) einer radioaktiven Quelle ist umso höher, je mehr unzerfallene Kerne in der Quelle vorhanden sind.
- Die Aktivität \(A\) einer bestimmten Zahl unzerfallener Kerne ist umso höher, je größer die Zerfallswahrscheinlichkeit dieser Kerne ist. Das heißt, je kürzer die Halbwertszeit des Stoffes ist, desto höher ist die Aktivität.
Da die Kerne zeitlich unregelmäßig zerfallen, darf man für die Messung der Aktivität \(A\) nicht zu kurze Messzeiträume \(\Delta t\) wählen. Jedoch muss die Messzeit deutlich unter der Halbwertszeit \(T_{1/2}\) des Präparates liegen.
Anhand der Aktivität\(A\) einer Quelle kannst du noch keine Aussage darüber machen, welche Strahlenart(en) die Quelle emittiert und wie hoch deren Energie ist.
Alte Einheit "Curie"
Früher wurde die Aktivität in der Einheit Curie \(\rm{Ci}\) angegeben. Für die Umrechnung von Curie in Bequerel gilt \(1\,\rm{Ci}=3{,}7\cdot 10^{10}\,\rm{Bq}\).
Spezifische Aktivität
Um die Aktivität \(A\) von verschiedener Proben besser miteinander vergleichen zu können, berechnet man häufig das Verhältnis der Aktivität \(A\) zur Masse \(m\) der Probe. Dieses Verhältnis nennt man die spezifische Aktivität der Probe. Die SI-Einheit der spezifischen Aktivität ist \(\rm{\frac{Bq}{kg}}\).
Beispiele für einige spezifische Aktivitätswerte
Die folgenden Werte sind jeweils spezifische Aktivitäten. Die Werte geben also an, welche Aktivität \(A\) eine Probe der Masse \(m=1\,\rm{kg}\) besitzt.
| Pflanzliche und tierische Nahrungsmittel | \(\text{ca. }40\,\rm{\frac{Bq}{kg}}\) |
| Natururan | \(12\cdot 10^{6}\,\rm{\frac{Bq}{kg}}\) |
| Uran-235 | \(80\cdot 10^6\,\rm{\frac{Bq}{kg}}\) |
| Radium-226 | \(3{,}7\cdot 10^{13}\,\rm{\frac{Bq}{kg}}\) |
Aktivität des Menschen
Auch der Mensch strahlt. Der Standard-Mensch, etwa \(70\,\rm{kg}\) schwer und zwischen 20 und 30 Jahre alt, hat eine Aktivität von etwa \(A_{\rm{Mensch}}=9100\,\rm{Bq}\). Dies entspricht einem Mittelwert der spezifischen Aktivität von \(130\,\rm{\frac{Bq}{kg}}\).
|
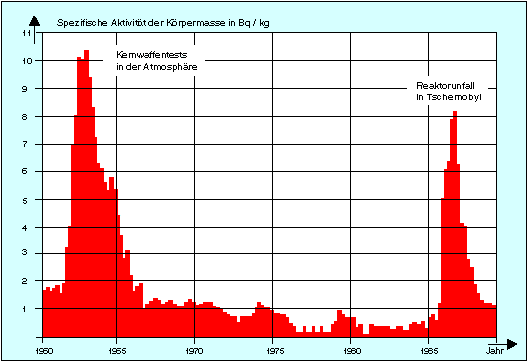
In der nebenstehenden Abbildung ist die auf ein Kilogramm bezogene Aktivität (spezifische Aktivität) des Menschen in der BRD, welche nur vom Isotop Cs-137 verursacht wird, in Abhängigkeit von der Zeit dargestellt. Man sieht, dass die spezifische Cs-Aktivität zur Zeit der Kernwaffentests in sechziger Jahren des 20. Jahrhunderts und im Jahr 1986 bei der Reaktorkatastrophe von Tschernobyl besonders hoch war. Hinweis |
|
Aufgabe
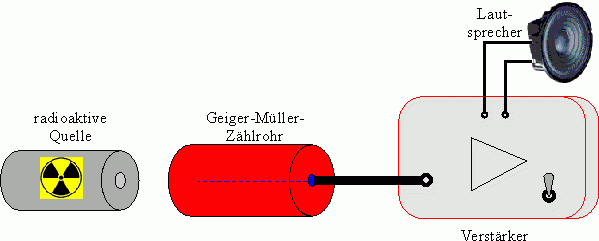
Flexon möchte mit nebenstehender Anordnung - unter Verwendung des Geiger-Müller-Zählrohrs der Schule - die Aktivität \(A\) einer radioaktiven Quelle bestimmen.
a)Erläutere, warum Flexon mit der Anordnung in Abb. 2 die Aktivität \(A\) einer Quelle nicht exakt bestimmen kann.
b)Erläutere, was Flexon bei der Messung alles bedenken müsste, wenn er die Aktivität der Quelle nur annähernd abschätzen will.