Eine genauere Bestimmung der Neutronenmasse als über die Methode der Rückstoßkerne bietet die Betrachtung von Kernreaktionen. Chadwick und Goldhaber nutzten 1934 für die Photospaltung des Deuterons in seine Bestandteile Neutron und Proton die 2,62-MeV-Gammastrahlung eines Thoriumisotops. In eine Ionisationskammer, wie er sie schon bei seinem "Rückstoß-Versuch" nutzte, leitete Chadwick Deuteriumgas ein und bestrahlte es mit den Gammaquanten. In der Nachweisapparatur zeigten sich daraufhin kräftige Impulse, die auf die Ionisation der als Zerfallsprodukt entstandenen schnellen Protonen zurückzuführen waren.
\[{}_1^2{\rm{D}} + {}_0^0{\rm{\gamma }} \to {}_0^1{\rm{n}} + {}_1^1{\rm{p}}\]
Während Chadwick und Goldhaber aus der kinetischen Energie des Protons und des Neutrons (Annahme: Ekin,p = Ekin,n) auf die Neutronenmasse schlossen, zielen spätere, noch genauere Experimente auf die Bestimmung der Bindungsenergie des Deuterons ab.
Versuch von Mobley und Laubenstein (1950)
The photo-neutron thresholds of beryllium and deuterium have been measured by comparison with the Li7(p,n) threshold. For this purpose an electrostatic generator was used in which an electron beam and a positive ion beam were established simultaneously. Accurate control and measurement of the generator voltage was obtained by using an electrostatic analyzer on the H2+ component of the ion beam. Because the Li7(p,n) threshold lies between the Be9(γ,n) and D(γ,n) thresholds, errors in extrapolation should be small. The electron beam was accelerated from ground to the accurately known potential of the high voltage electrode where x-rays were produced for the photo-disintegration process. From the photo-neutron thresholds the neutron binding energies of beryllium and deuterium were found to be 1.666 ± 0.002 and 2.226 ± 0.003 Mev, respectively. ©1950 The American Physical Society |
|
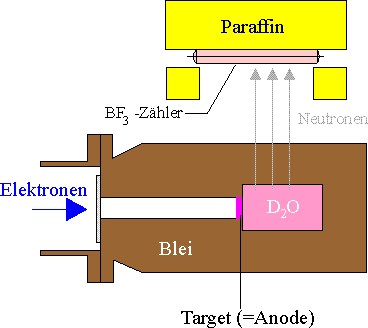
Mit einer "Röntgenröhre", deren Spannung bis über 2 MV kontinuierlich verändert werden kann, treffen die Elektronen auf ein Target (Anode) und erzeugen ein kontinuierliches Röntgenbremsspektrum mit einer scharfen kurzwelligen Grenze bei λG. |
 |
|
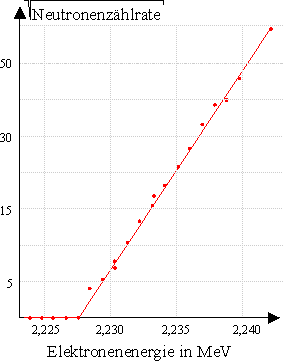
Man sieht aus dem Diagramm, dass das Deuterium bei einer Elektronenenergie (= Energie des energiereichsten Gammaquants) von ca. 2,227 MeV zerfällt. Diese Energie ist zugleich die Bindungsenergie B des Deuterons, für die gilt |
 |

