RUTHERFORD und seine Schüler waren die ersten, welche die von radioaktiven Präparaten ausgesandten α-Teilchen als Kerngeschosse verwandten. Bei diesen Experimenten wurden die α-Teilchen elastisch gestreut, d.h. es kam zu keiner Anregung oder Veränderung des Kerns.
Da die verwendeten α-Teilchen nur eine kinetische Energie von ca. \(6\rm{MeV}\) besaßen und die Kernladungszahl von Gold sehr groß ist (\(Z = 79\)), ist zu vermuten, dass die Geschosse noch nicht in den unmittelbaren Kernbereich gelangen, wo dann eine Auswirkung der Kernkräfte zu beobachten sein müsste. RUTHERFORD ging in seiner theoretischen Berechnung der Streuverteilung tatsächlich von einer reinen COULOMB-Wechselwirkung aus und stellte eine sehr gute Übereinstimmung mit den experimentellen Ergebnissen fest.
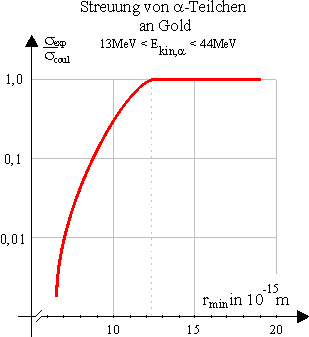
Die Wahrscheinlichkeit, dass ein Teilchen in eine vorgegebene Richtung gestreut wird, beschreibt man durch den differentiellen Wirkungsquerschnitt \({\sigma _{{\rm{exp}}}}\). In der nebenstehenden Abbildung ist auf der Hochwertachse (logarithmischer Maßstab!) das Verhältnis des experimentell ermittelten Wirkungsquerschnitts bei der elastischen Streuung von α-Teilchen an Gold in Bezug zum theoretisch ermittelten Wirkungsquerschnitt \({\sigma _{{\rm{COULOMB}}}}\) dargestellt.
\({\sigma _{{\rm{COULOMB}}}}\) beschreibt die Streuverteilung, wenn ausschließlich COULOMB-Wechselwirkung zwischen den α-Teilchen und den Goldkernen vorliegen würde. Auf der Rechtswertachse der Abbildung ist der kleinste Abstand der Geschossteilchen vom Streuzentrum aufgetragen. Dieser kleinste Abstand würde erreicht, wenn die α-Teilchen zentral auf die Goldkerne zufliegen würden. Dieser Abstand ist umso kleiner, je größer die kinetische Energie der Geschosse ist.
Aus der Graphik ist ersichtlich, dass bei nicht zu hohen kinetischen Energien der α-Teilchen (d.h bei größeren \({r_{{\rm{min}}}}\)) der experimentell ermittelte Wirkungsquerschnitt und der - bei vorausgesetzter COULOMB-Wechselwirkung - berechnete Wirkungsquerschnitt gut übereinstimmen, d.h. die α-Teilchen erfahren wohl ausschließlich elektrostatische Kräfte.
Für kleinere Minimalabstände, d.h. bei größeren kinetischen Energien der α-Teilchen, differieren die beiden Wirkungsquerschnitte stark. Daraus kann man folgern, dass die Wechselwirkung zwischen den Geschossen und den Goldkernen nicht mehr rein elektrostatisch ist. Offensichtlich kommen die α-Teilchen den Kernen so nahe, dass bereits die Kernkräfte wirken. Dies lässt wiederum einen ungefähren Rückschluss auf den Kernradius zu.
Aus obigem Versuch kann man erkennen, dass gilt
\[{r_{{\rm{Kern}}}}({\rm{Au}}) + {r_{{\rm{Kern}}}}({\rm{He}}) \approx 12 \cdot {10^{ - 15}}{\rm{m}}\]
Ermittlung des Kernradius aus der elastischen Streuung von Elektronen

Robert HOFSTADTER (1915 - 1990)
von Nobel foundation [Public domain], via Wikimedia Commons
Ein sehr erfolgreiches Experiment zur Untersuchung der Kerngröße (genauer: zur Untersuchung der Ladungsverteilung im Kern) gelang im Jahre 1953 Robert HOFSTADTER (1915 - 1990). Er benutzte als Geschosse Elektronen, welche den Vorteil hatten, dass sie nicht der starken Wechselwirkung, sondern nur der elektromagnetischen Wechselwirkung unterliegen.
Damit diese Projektile nicht durch die Atomhülle gestört werden und sie für die Untersuchung von Strukturen in der Größenordnung von \({10^{ - 15}}{\rm{m}} = 1{\rm{fm}}\) (1 Femtometer, auch 1 Fermi) geeignet sind, benötigte HOFSTADTER sehr energiereiche Elektronen (d.h. Elektronen mit einer kleinen de-BROGLIE-Wellenlänge), die er von dem damals weltweit größten Linearbeschleuniger (Länge ca. \(3\rm{km}\)) in Stanford erhielt. HOFSTADTER benutzte Elektronen, deren kinetische Energie zwischen \(250\rm{MeV}\) und einigen \(\rm{GeV}\) lag.
Eine Biographie von Robert HOFSTADTER finden Sie unter der Adresse http://www.nobel.se/physics/laureates/1961/hofstadter-bio.html. Von dieser Seite gelangen Sie dann auch zum Nobel-Vortrag Hofstadters (pdf-Datei).
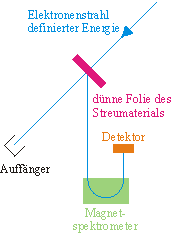

Die nebenstehende Abbildung zeigt den prinzipiellen Aufbau des Experiments: Der durch einen Magneten aus dem Beschleuniger herausgelenkte Elektronenstrahl trifft auf eine dünne Folie des zu untersuchenden Elements. Um diese Folie kann ein \(180^\circ \)-Magnetspektrometer geschwenkt werden. Als Detektor dient ein Photomultiplier.
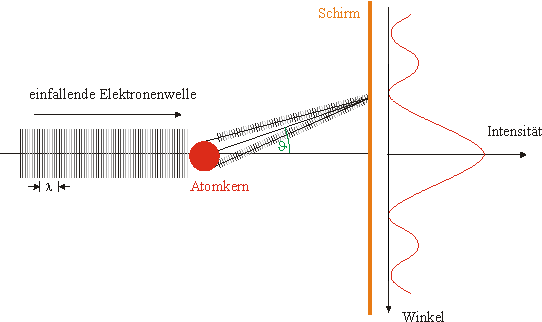
Man kann den einfallenden und den gestreuten Elektronen de-Broglie-Wellen zuordnen. Da es sich um eine elastische Streuung handelt, bleibt die Wellenlänge unverändert. Die vom Kern ausgehenden Streuwellen können - ähnlich wie beim Einfachspalt in der Wellenoptik - interferieren. Das Beugungsbild ist rot dargestellt.
Für den Winkel, bei dem das erste Minimum im Beugungsbild auftritt, gilt eine Beziehung, die der beim Einzelspalt sehr ähnlich ist (\(r\): Kernradius; \(\lambda\): de-BROGLIE-Wellenlänge):
\[\sin \left( \vartheta \right) = 0,61 \cdot \frac{\lambda }{r} \Leftrightarrow r = 0,61 \cdot \frac{\lambda }{{\sin \left( \vartheta \right)}}\]
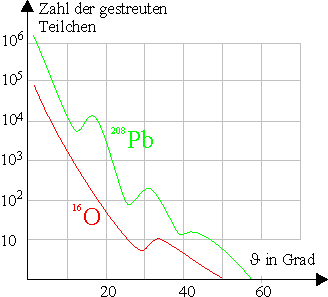
Die nebenstehende Abbildung zeigt die Beugungsbilder von mit \(500\rm{MeV}\) beschleunigten Elektronen bei der Streuung an Blei bzw. Sauerstoff.
-
Ermittle durch relativistische Rechnung die de-BROGLIE-Wellenlänge der Elektronen.
-
Ermittle mit Hilfe der Graphik den Radius des Bleikerns und Sauerstoffkerns.
Hinweis: Durch das HOFSTADTER-Experiment erhält man Aussagen über die Ladungsverteilung. Üblicherweise setzt man die Ausdehnung der Ladungsverteilung der Kernausdehnung gleich.
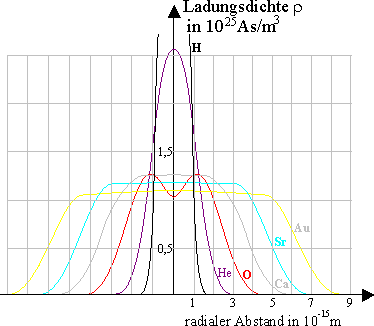
Aus den Streudaten für die Elektronen ergab sich die nebenstehende Darstellung für die Ladungsverteilung von Atomkernen. Auf der Hochwertachse ist die Dichte der positiven Ladung, auf der Rechtswertachse der radiale Abstand vom Kernzentrum aufgetragen.
Neben dem Beschuss mit α-Teilchen (starke und elektromagnetische Wechselwirkung) und Elektronen (elektromagnetische Wechselwirkung) hat man auch Streuexperimente mit Neutronen (starke Wechselwirkung) am Kern durchgeführt. Alle Experimente ergaben Kernradien, die näherungsweise durch die folgende empirische Formel beschrieben werden können:
\[{r_{{\rm{Kern}}}} = {r_0} \cdot \sqrt[3]{A}\;{\rm{mit}}\;A{\rm{:}}\;{\rm{Massezahl}}\;{\rm{;}}\;{r_0} \approx 1,4 \cdot {10^{ - 15}}{\rm{m}}\]
Dabei entspricht \({r_0}\) in etwa dem Protonenradius.

