In der Atomphysik haben wir andeutungsweise den historischen Weg vom einfachen Atommodell der kinetischen Gastheorie bis hin zum quantenmechanischen Atommodell verfolgen können. Letzteres ist extrem leistungsfähig und beschreibt - bei entsprechendem mathematischen Aufwand, der an Schulen nicht nachvollzogen werden kann - alle Eigenschaften der Atomhülle erschöpfend.
In der Kernphysik fehlt noch das allumfassende Modell. Man verwendet für die Beschreibung unterschiedlicher Kerneigenschaften meist auch unterschiedliche Modelle. Ein Modell ist das Tröpfchenmodell, ein zweites das Potentialtopfmodell für Atomkerne.
Tröpfchenmodell
Das Tröpfchenmodell behandelt den Kern ähnlich wie einen Flüssigkeitstropfen, bei dem man auch von einer konstanten Materiedichte ausgehen kann. Dieses Modell verschafft eine Einsicht in den Verlauf der Bindungsenergie eines Kerns und damit dessen Masse. Das Modell ist in der Lage einige Aussagen über Kernzerfälle und auch Spaltreaktionen zu machen. Weitergehende Vorhersagen kann die sogenannte semiempirische Massenformel von Weizäcker jedoch nicht leisten.
Die Idee zum Tröpfchenmodell stammt von dem Physiker GAMOV und wurde von mehreren namhaften Physikern (u.a. BETHE und v. WEIZSÄCKER) weiterentwickelt.
Die Ruhemasse eines Kerns kann mit Hilfe der Bindungsenergie in der folgenden Form geschrieben werden: \[{m_{{\rm{K}}{\rm{,0}}}} = Z \cdot {m_{p,0}} + N \cdot {m_{n,0}} - \frac{B}{{{c^2}}}\] Wenn es gelingt, \(B\) zu berechnen, so kann man alle Kernmassen theoretisch vorhersagen. Durch einen Vergleich mit einem Flüssigkeitstropfen konnte v. WEIZSÄCKER eine halbempirische Formel für \(B\) angeben. In Folge verschiedener Einflüsse setzt sich die Bindungsenergie (entspricht beim Flüssigkeitstropfen etwa der Kondensationsenergie) aus verschiedenen Anteilen zusammen: \[B = {B_0} + {B_1} + {B_2} + ...\] Auf die leichter verständlichen Anteile der Bindungsenergie wird im Folgenden eingegangen.
Volumenenergie
Der größte Anteil \({{B_0}}\) der Bindungsenergie ist auf die direkte kurzreichweitige Wechselwirkung der Nukleonen aufgrund der Kernkräfte zurückzuführen. Aus dem Verlauf der mittleren Bindungsenergie pro Nukleon in Abhängigkeit von \(A\) weiß man, dass für mittlere Kerne eine Wert für \(\frac{B}{A}\) von ungefähr \(8\,\rm{MeV}\) anzusetzen ist (bei sehr leichten und sehr schweren Kernen sind noch andere Einflüsse zu berücksichtigen).
Die Massendichte in den Kernen ist nahezu unabhängig von deren Massezahl (vgl. hierzu Musteraufgabe). Dies ist eine unmittelbare Folge der Kurzreichweitigkeit der Kernkräfte. Jedes Nukleon tritt nur mit seinen unmittelbaren Nachbarn in direkte Wechselwirkung und deren Zahl ist begrenzt. Die Bindungsenergie für ein Nukleon hängt also nicht davon ab, wie viele Nukleonen noch jenseits der unmittelbaren Nachbarn vorhanden sind. Es gilt\[\frac{{{B_0}}}{A} = {\rm{const}}{\rm{.}} \Rightarrow {B_0} \sim A \Rightarrow {B_0} = {a_{\rm{V}}} \cdot A\]
Oberflächenenergie
Die strenge (direkte) Proportionalität zwischen \({{B_0}}\) und \(A\) geht davon aus, dass jedes Nukleon stets die gleichartige Umgebung vorfindet. Dies ist jedoch für Nukleonen an der Kernoberfläche nicht der Fall, sie sind nicht - aufgrund fehlender Partner - so stark gebunden wie Nukleonen im Kerninneren. Man muss daher den Term Bo durch den sogenannten Oberflächenterm B1 korrigieren. Die Zahl der Nukleonen an der Kernoberfläche ist proportional zur Oberfläche: \(N\sim O\). Für die Abhängigkeit der Oberfläche von der Nukleonenzahl lässt sich die folgende Proportionalität angeben: \[O = 4 \cdot \pi \cdot {r_{\rm{K}}}^2 = 4 \cdot \pi \cdot {\left( {{r_{\rm{0}}} \cdot \sqrt[3]{A}} \right)^2} = 4 \cdot \pi \cdot {r_{\rm{0}}}^2 \cdot {A^{\frac{2}{3}}} \Rightarrow O \sim {A^{\frac{2}{3}}}\] Somit ergibt sich als Korrekturterm für die Volumenenergie \[{B_1} = - {a_{\rm{O}}} \cdot {A^{\frac{2}{3}}}\]
COULOMB-Energie
Die im Kern befindlichen Protonen stoßen sich aufgrund der langreichweitigen Coulombkräfte gegenseitig ab. Auch dies führt zu einer Verringerung der Bindungsenergie, was in einem weiteren Korrekturterm \(B_2\) berücksichtigt wird. Für die elektrostatische Energie einer kontinuierlich über das Innere einer Kugel vom Radius \({r_{\rm{K}}}\) verteilte Gesamtladung \(Z \cdot e\) gilt \[{E_{estat}} \sim \frac{{{{\left( {Z \cdot e} \right)}^2}}}{{{r_{\rm{K}}}}} = \frac{{{{\left( {Z \cdot e} \right)}^2}}}{{{r_{\rm{0}}} \cdot \sqrt[3]{A}}} = \frac{{{e^2} \cdot {Z^2}}}{{{r_{\rm{0}}}}} \cdot {A^{ - \frac{1}{3}}} \Rightarrow {E_{estat}} \sim {Z^2} \cdot {A^{ - \frac{1}{3}}}\] Somit ergibt sich als Korrekturterm für die COULOMB-Energie \[{B_2} = - {a_{\rm{C}}} \cdot {Z^2} \cdot {A^{ - \frac{1}{3}}}\]
Von WEIZSÄCKER führte noch weitere Korrekturterme ein, auf die hier nur kurz eingegangen werden soll: Mit der Asymmetrieenergie wird dem Neutronenüberschuss schwerer Kerne Rechnung getragen und mit der Paarungsenergie wird die Tatsache berücksichtigt, dass Kerne mit gerader Neutronen- und Protonenzahl (gg-Kerne) deutlich stabiler sind als solche mit ungerader Neutronen- und Protonenzahl (uu-Kerne). Die folgende Tabelle gibt hierüber einen statistischen Überblick:
| Kernsorte | Zahl der stabilen Isotope | Stabilität | Zahl der Isotope pro Element |
| gg: gerade Protonen- und Neutronenzahl | 165 | sehr stabil | mehrere |
| gu: gerade Protonenzahl und ungerade Neutronenzahl | 55 | stabil | 1 |
| ug: ungerade Protonenzahl und gerade Neutronenzahl | 50 | stabil | 1 |
| uu: ungerade Protonen- und Neutronenzahl | 4 | zumeist instabil | 1 |
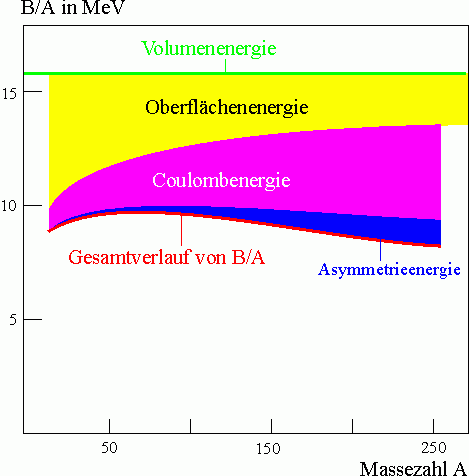
Beiträge der einzelnen Energieterme
In der Skizze in Abb. 4 sind die einzelnen Beiträge der Energieterme zur gesamten Bindungsenergie pro Nukleon B/A dargestellt. Die Proportionalitätskonstanten aV, aO, aC usw. sind dabei empirisch ermittelte Werte.