Der Widerstand eines elektrischen Leiters hängt neben seiner Länge und seiner Querschnittsfläche natürlich auch vom Material des Leiters ab. Jedes Material besitzt einen sog. spezifische Widerstand \(\rho\) (gesprochen: "rho"). Der spezifische Widerstand \(\rho\) ist also eine Materialkonstante.
Den Widerstand \(R\) eines Leiters mit der Länge \(l\), der Querschnittsfläche \(A\) und aus einem Material mit dem spezifischen Widerstand \(\rho\) berechnest du mittels\[R=\rho\cdot\frac{l}{A}\]
Der Widerstand des Leiters ist also proportional zum spezifischen Widerstand des Materials. Je größer der spezifische Widerstand eines Materials ist, desto größer ist der Widerstand eines Drahtstücks und um so schlechter leitet das Material elektrischen Strom.
Widerstand eines Drahtes und spezifischer Widerstand
Für den Widerstand eines Drahtes der Länge \(l\), der Querschnittsfläche \(A\) und aus einem Material mit dem spezifischen Widerstand \(\rho\) gilt:\[R=\rho\cdot \frac{l}{A}\]Entsprechend kannst du den spezifischen Widerstand \(\rho\) eines Leiters berechnen mit \[\rho=\frac{R\cdot A}{l}\]Für die Einheit des spezifischen Widerstandes erhältst du dabei \([\rho]=\frac{\Omega\cdot \rm{mm^2}}{\rm{m}}\).
Veranschaulichung des Einflusses der Größen
Den Einfluss der einzelnen Größe auf den Widerstand eines Drahtes und damit auf die Stromstärke, die sich bei fester Spannung ergibt, kannst du dir mit Hilfe der Simulation in Abb. 1 gut veranschaulichen.
Hinweis: Die Länge des Kabels, von uns meist mit \(l\) bezeichnet, ist hier mit dem Großbuchstaben \(L\) bezeichnet.
Spezifischer Widerstand verschiedener Materialien
Die folgende Tabelle gibt die spezifischen Widerstände einiger ausgesuchter Materialien an:
| Material | Silber | Kupfer | Aluminium | Stahl | Konstantan | Kohle | Porzellan |
|---|---|---|---|---|---|---|---|
| spezifischer Widerstand \(\rho \;{\rm{in}}\;\frac{{\Omega \cdot {\rm{m}}{{\rm{m}}^2}}}{{\rm{m}}}\) | \(0{,}016\) | \(0{,}017\) | \(0{,}028\) | \(0{,}13\) | \(0{,}50\) | \(40\) | \(5 \cdot {10^{18}}\) |
Silber und Kupfer sind also sehr gute Leiter, da sie nur einen geringen spezifischen Widerstand besitzen. Porzellan hingegen ist mit seinem extrem hohen spezifischen Widerstand ein sehr guter Isolator. Weiter ist der spezifische Widerstand temperaturabhängig. Die angegebenen Werte gelten also nur bei fester Temperatur des Leiters.
Achtung: Verwechsle den spezifischen Widerstand \(\rho\) nicht mit der Dichte eines Körpers. Die Dichte hat zwar ebenfalls das Formelzeichen \(\rho\), beschreibt aber physikalisch etwas ganz anderes und wird in der Einheit \(\frac{g}{{{\rm{c}}{{\rm{m}}^3}}}\) angegeben.
Experimentelle Bestimmung des spezifischen Widerstands
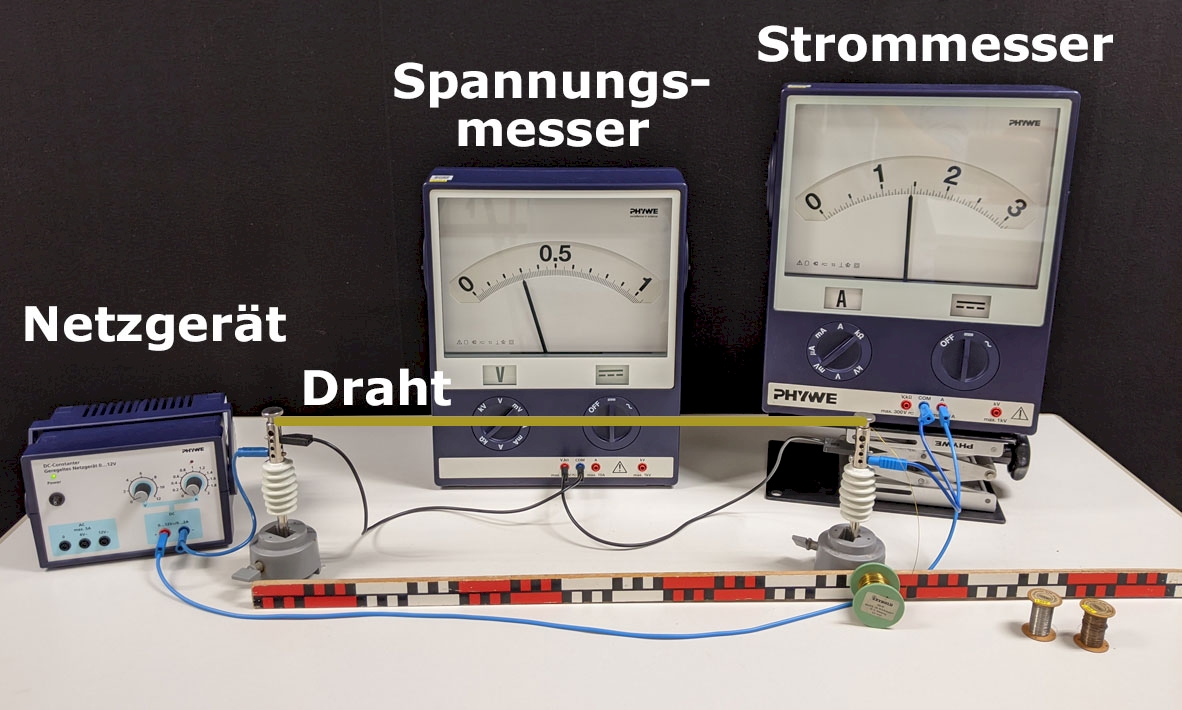
Mit Experimenten wie in Abb. 2 kannst du den Einfluss der Länge \(l\) und der Querschnittsfläche \(A\) eines Drahtes auf seinen Widerstand \(R\) bestimmen. Dabei zeigt sich, dass der Widerstand \(R\) eines Drahtes proportional zu seiner Länge \(l\) ist, also \(R\sim l\) gilt. Weiter ist der Widerstand \(R\) entgegengesetzt proportional zur Querschnittsfläche \(A\) des Leiters. Es gilt also \(R\sim\frac{1}{A}\).
Die beide Proportionalitäten \(R\sim l\) und \(R\sim\frac{1}{A}\) kannst du zusammenfassen zu \[R\sim\frac{l}{A}\]Um von der Proportionalitätsaussage zu einer Gleichung zu gelangen, führst du eine Proportionalitätskonstante ein, den spezifischen Widerstand \(\rho\). In diese Größe gehen die spezifischen Eigenschaften des verwendeten Drahtmaterials ein. Somit gilt für den Widerstand eines Leiters allgemein:\[R=\rho\cdot\frac{l}{A}\]
Verständnisaufgabe
Verständnisaufgabe
Markiere alle physikalisch richtigen Aussagen.