Bei dem technischen Wechselstrom, wie ihn uns die Elektrizitätswerke liefern, ist die Frequenz \(f = 50\,{\rm{Hz}}\). Es erfolgt also alle \(0{,}01\,{\rm{s}}\) ein Polwechsel an der Steckdose. Zwischen zwei Polwechseln nehmen Stromstärke bzw. Spannung an einem angeschlossenen Widerstand mit dem Wert \(R\) alle Werte zwischen Null und dem Scheitelwert \(\hat I\) bzw. \(\hat U\) an. Momentane Strom- bzw. Spannungswerte sind ebenso wie die Scheitelwerte im allgemeinen nur von untergeordneter Bedeutung.
Wesentlich ist dagegen die gelieferte Energie, die man aber wegen der wechselnden Werte von Stromstärke und Spannung nicht mehr mit der Formel \({W_{{\rm{el}}}} = U \cdot I \cdot t\) berechnen kann. Man führte deshalb bei Wechselströmen die Begriffe effektive Stromstärke und effektive Spannung ein.
Effektivwerte von Wechselstrom und -spannung
Unter dem Effektivwert \({{U_{\rm{eff}}}}\) einer Wechselspannung versteht man diejenige zeitlich konstante Spannung (Gleichspannung), die am gleichen Widerstand \(R\) in der gleichen Zeit die gleiche Energie wie die Wechselspannung liefert.
Unter dem Effektivwert \({{I_{\rm{eff}}}}\) eines Wechselstroms versteht man diejenige zeitlich konstante Stromstärke (Stromstärke eines Gleichstroms), die am gleichen Widerstand \(R\) in der gleichen Zeit die gleiche Energie wie der Wechselstrom liefert.
Bestimmung der Effektivwerte \({{U_{\rm{eff}}}}\) und \({{I_{\rm{eff}}}}\) durch eine geometrische Betrachtung
Bei einer zeitlich konstanten Leistung (also bei Gleichstrom) berechnet man die während der Periodendauer \(T\) gelieferte elektrische Energie nach
\[{W_{{\rm{el}}}} = P \cdot T\]
Für die Berechnung der Energie beim Wechselstrom müsste man die Integralrechnung bemühen:
\[{W_{{\rm{el}}}} = \int\limits_0^T {P(t)d} t\]
Da dir eventuell die Integralrechnung noch nicht geläufig ist, versuchen wir die Effektivwerte von Spannung und Strom durch eine geometrische Betrachtung zu gewinnen. Dabei nutzen wir aus, dass in einem Zeit-Leistungs-Diagramm die Fläche unter der Kurve die elektrische Arbeit (bzw. Energie) darstellt. Für die momentane Leistung an einem ohmschen Widerstand, an dem die zeitlich veränderliche Spannung \(U(t)\) liegt, gilt
\[P(t) = U(t) \cdot I(t) = R \cdot I{(t)^2} = \frac{{U{{(t)}^2}}}{R}\]
Bei einer sinusförmigen Wechselspannung gilt dann insbesondere
\[P(t) = \hat U \cdot \sin \left( {\omega \cdot t} \right) \cdot \hat I \cdot \sin \left( {\omega \cdot t} \right) = \hat U \cdot \widehat I \cdot {\left( {\sin \left( {\omega \cdot t} \right)} \right)^2}\]
oder
\[P(t) = \frac{{{{\hat U}^2}}}{R} \cdot {\left( {\sin \left( {\omega \cdot t} \right)} \right)^2} \quad (1) \quad \text{bzw.}\quad P(t) = {{\hat I}^2} \cdot R \cdot {\left( {\sin \left( {\omega \cdot t} \right)} \right)^2}\]
Der zeitliche Verlauf der Leistung, wie sie in Gleichung \((1)\) beschrieben ist, wird in der Animation dargestellt.
Zeitlicher Verlauf von Leistung, Spannung und Stromstärke
Die Animation veranschaulicht, dass die durch die sinusförmige Wechselspannung am Widerstand \(R\) in der Zeit \(T\) verrichtete elektrische Arbeit in einen gleichgroßen Arbeitsbetrag umgewandelt werden kann, der von einer Gleichspannung bewirkt wird, der oben definierten Effektivspannung \({{U_{\rm{eff}}}}\). Für den Zusammenhang zwischen dem Scheitelwert der Wechselspannung \({\hat U}\) und dem Effektivwert \({{U_{\rm{eff}}}}\) gilt
\[{\bar P \cdot T = \frac{1}{2} \cdot \frac{{{{\hat U}^2}}}{R} \cdot T \Leftrightarrow \frac{{U_{\rm{eff}}^2}}{R} \cdot T = \frac{1}{2} \cdot \frac{{{{\hat U}^2}}}{R} \cdot T \Leftrightarrow U_{\rm{eff}}^2 = \frac{1}{2} \cdot {{\hat U}^2}}\]
Daraus erhält man
\[{{U_{\rm{eff}}} = \frac{{\hat U}}{{\sqrt 2 }}}\]
Analog gilt für den Effektivwert des Stroms
\[{I_{\rm{eff}}} = \frac{{\hat I}}{{\sqrt 2 }}\]
Effektivwerte von sinusförmigem Wechselstrom bzw. sinusförmiger Wechselspannung
Für den Effektivwert \({{U_{\rm{eff}}}}\) einer sinusförmigen Wechselspannung mit dem Scheitelwert \({\hat U}\) gilt\[{{U_{\rm{eff}}} = \frac{{\hat U}}{{\sqrt 2 }}}\].
Für den Effektivwert \({{I_{\rm{eff}}}}\) eines sinusförmigen Wechselstroms mit dem Scheitelwert \({\hat I}\) gilt\[{I_{\rm{eff}}} = \frac{{\hat I}}{{\sqrt 2 }}\]
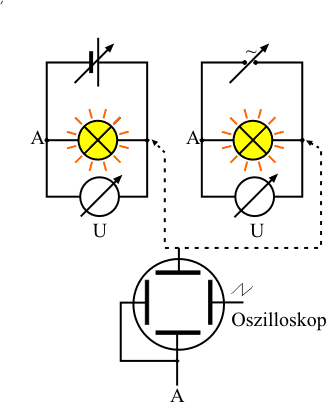
Nachweis im Experiment
Die Beziehung \({U_{\rm{eff}}} = \frac{{\hat U}}{{\sqrt 2 }}\) kann mit folgendem Versuch angenähert bestätigt werden:
Zwei Lämpchen gleicher Bauart werden durch eine Gleich- bzw. Wechselspannungsquelle betrieben. Die Spannungen werden so gewählt, dass die Lämpchen gleich hell leuchten.
Schaltet man parallel zu den Lämpchen ein Gleichspannungs- bzw. ein in Effektivwerten geeichtes Wechselspannungs-Voltmeter, so erhält man beide Male den gleichen Spannungswert.
Die Darstellung beider Spannungen am Oszilloskop ergibt, dass der Scheitelwert der Wechselspannung etwa \(1{,}4 \approx \sqrt 2 \)-mal so groß ist wie der Wert der Gleichspannung.

