Aufbau
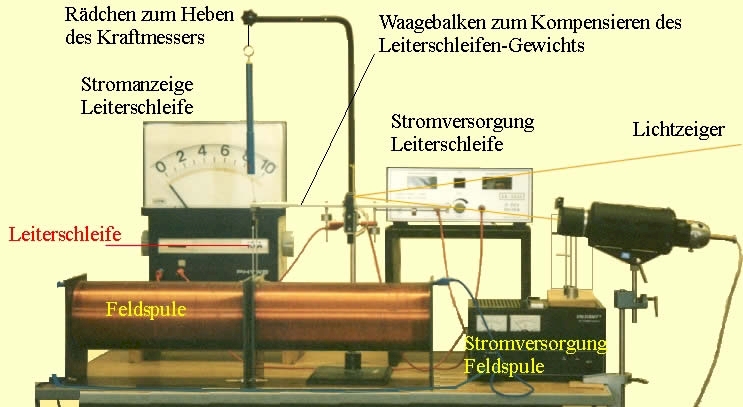
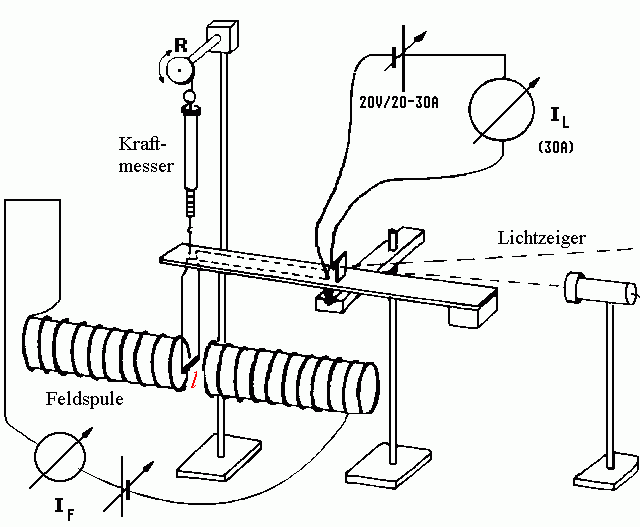
Versuchsgeräte
•Lange geteilte Feldspule mit Stromversorgung und Amperemeter \(I_{\rm{F}}\) bis \(10\,\rm{A}\)). Die Teilung der Spule ist erforderlich, damit die Leiterschleife in das homogene Magnetfeld zwischen den Spulenteilen eingeführt werden kann.
•Stromwaage mit Ausgleichsgewicht zum Ausbalancieren des Leiterschleifengewichts.
•Leiterschleife mit Stromversorgung (\(I_{\rm{L}}\) bis \(20\,\rm{A}\)) und Amperemeter
•Kraftmesser F im Bereich von mN mit Faden und Rädchen zum Verändern seiner Position
•Lampe mit Spiegelchen und Schirm als Lichtzeiger.
Eine Leiterschleife mit bekannter Leiterlänge \(l\) wird an die Stromwaage gesteckt und so in den Spalt der Feldspule gebracht, dass sich die Leiterlänge vollständig im Spuleninneren möglichst in der Mitte befindet und senkrecht zur Spulenachse ausgerichtet ist. Nun bringt man durch ein Ausgleichsgewicht den Waagebalken ins Gleichgewicht und gibt auf die Federwaage durch Drehen am Rädchen eine geringe Vorspannung. Dann schiebt man den Nullpunktschieber der Federwaage so, dass dieser auf \(0{,}0\,\rm{mN}\) steht. Diese Stellung wird über den Lichtzeiger an einer Marke an der Wand fixiert (Tesaband, Bleistift, Kreide). Der Feldstrom und damit das Magnetfeld wird während des gesamten Versuchs nicht geändert.
Erläuterungen zum Versuchsaufbau
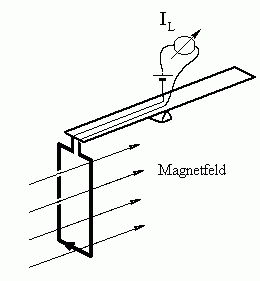
•Da sich die links- und rechtsgerichteten magnetischen Kräfte auf den Leiterrahmen aufheben, wirkt auf ihn, wenn das Magnetfeld wie in Abb. 4 aus der Zeichenebene heraus gerichtet ist, eine resultierende Kraft mit dem Betrag \(F_{\rm{m}}\) nach unten.
•Der Waagebalken soll während des gesamten Versuchs das Gewicht der Leiterschleife halten.
•Die Stellung der Leiterschleife im Magnetfeld sollte während des gesamten Versuchs immer gleich bleiben (Kontrollmöglichkeit durch den empfindlichen Lichtzeiger). Auf diese Weise spielen Inhomogenitäten des Magnetfeldes keine Rolle.
•Die magnetische Kraft \(F_{\rm{m}}\), welche bei eingeschaltetem Leiterstrom den Leiter nach unten ziehen würde, wird durch die Federwaage kompensiert. Dabei wird mit Hilfe des Rädchens \(R\) die Höhe der Federwaage so eingestellt, dass der Lichtzeiger und somit auch der Waagbalken in seiner ursprünglichen Stellung bleibt.
•In diesem Fall ist die magnetische Kraft gleich der vom Kraftmesser angezeigten Kraft.
•Würde man die Leiterschleife direkt an eine Federwaage hängen, müsste man eine für das Gesamtgewicht der Leiterschleife (im 100 mN - Bereich) geeignete Federwaage verwenden, die 100-fach gröber misst als die verwendete Federwaage, die im mN-Bereich misst.
Durchführung
Man lässt bei eingeschaltetem Magnetfeld durch den Leiter Strom fließen, wobei zunächst die Leiterschleife mit dem Waagebalken aus dem Gleichgewicht nach unten gezogen wird. Durch Drehen am Rädchen zieht man die Federwaage so lange hoch, bis der Lichtzeiger wieder seine Anfangsstellung einnimmt. Nun kann man die die magnetische Kraft kompensierende Kraft an der Federwaage ablesen. Es werden zwei Versuchsreihen durchgeführt: Im ersten Teilversuch untersucht man die Abhängigkeit der magnetischen Kraft \(F_{\rm{m}}\) vom Leiterstrom \({I_{\rm{L}}}\) bei gleichbleibender Leiterlänge, im zweiten Teilversuch die Abhängigkeit der magnetischen Kraft \(F_{\rm{m}}\) von der Leiterlänge \(l\) bei gleichbleibendem Leiterstrom \({I_{\rm{L}}}\).
Beobachtung
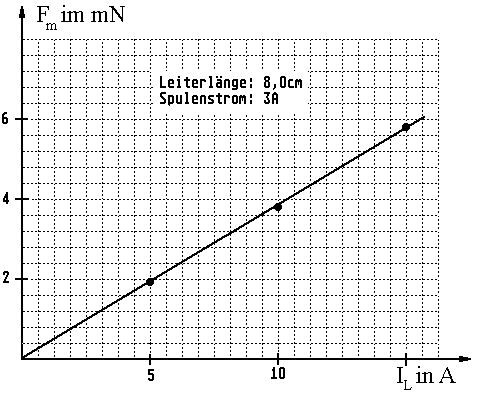
1. Teilversuch: Abhängigkeit der magnetischen Kraft \(F_{\rm{m}}\) vom Leiterstrom \({I_{\rm{L}}}\) bei gleichbleibender Leiterlänge (\(l=8\,\rm{cm}\))
| \({I_{\rm{L}}}\;{\rm{in}}\;{\rm{A}}\) | 5,0 | 10 | 15 |
| \({F_{\rm{m}}}\;{\rm{in}}\;{\rm{mN}}\) | 1,9 | 3,8 | 5,8 |
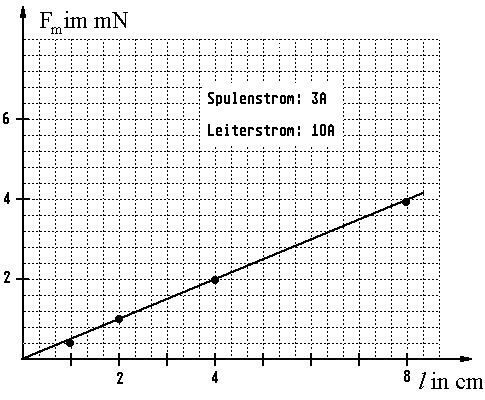
2. Teilversuch: Abhängigkeit der magnetischen Kraft \(F_{\rm{m}}\) von der Leiterlänge \(l\) bei gleichbleibendem Leiterstrom \({I_{\rm{L}}}\) (\({I_{\rm{L}}}=10\,\rm{A}\))
| \(l\;{\rm{in}}\;{\rm{cm}}\) | 1,0 | 2,0 | 4,0 | 8,0 |
| \({F_{\rm{m}}}\;{\rm{in}}\;{\rm{mN}}\) | 0,4 | 0,9 | 2,0 | 3,8 |
Auswertung
Die Versuchsauswertung erfolgt graphisch in Form eines \(I_{\rm{L}}\text{-}F_{\rm{m}}\)-Diagramms bzw. eines \(l\text{-}F_{\rm{m}}\)-Diagramms.
Auswertung des 1. Teilversuchs: Abhängigkeit der magnetischen Kraft \({F_m}\) vom Leiterstrom \({I_L}\) bei gleichbleibender Leiterlänge (\(l=8\rm{cm}\)). Der lineare Verlauf des Diagramms zeigt, dass \({F_{\rm{m}}} \sim {I_{\rm{L}}}\) ist.
Auswertung des 2. Teilversuch: Abhängigkeit der magnetischen Kraft \({F_m}\) von der Leiterlänge \(l\) bei gleichbleibendem Leiterstrom \({I_L}\) (\({I_L}=10\rm{A}\)). Der lineare Verlauf des Diagramms zeigt, dass \({F_{\rm{m}}} \sim l\) ist.
Versuchsdeutung
Die beiden Proportionalitäten \({F_{\rm{m}}} \sim {I_{\rm{L}}}\) (bei \(I\) konstant) und \({F_{\rm{m}}} \sim l\) (bei \({I_{\rm{L}}}\) konstant) kann man zu einer Proportionalität zusammenfassen:
\[{F_{\rm{m}}} \sim {I_{\rm{L}}} \cdot l\]
Durch Einführen einer Proportionalitätskonstante, die in diesem Fall mit \(B\) bezeichnet wird, kann die Proportionalität in eine Gleichung übergeführt werden:
\[{F_{\rm{m}}} = B \cdot {I_{\rm{L}}} \cdot l\]
Zunächst könnte man der Meinung sein, dass die magnetische Kraft \({F_{\rm{m}}}\) eine geeignete Größe sei, um die "Stärke" des Magnetfeldes der Feldspule zu beschreiben. Wie die letzte Gleichung jedoch zeigt, hängt \(F_{\rm{m}}\) von Strom durch die Leiterschleife \({I_{\rm{L}}}\) und der Länge \(l\) der Leiterschleife ab, also von Parametern der Sonde, mit welcher das Magnetfeld untersucht wurde. Dividiert man obige Gleichung durch diese beiden Parameter, so erhält man die Größe \(B\), die nur noch von der Stärke des untersuchten Magnetfeldes abhängt:
\[{F_{\rm{m}}} = B \cdot {I_{\rm{L}}} \cdot l\;|\;\frac{1}{{{I_{\rm{L}}} \cdot l}} \Rightarrow \quad B = \frac{{{F_{\rm{m}}}}}{{{I_{\rm{L}}} \cdot l}}\]
\(B\) ist eine Vektorgröße, die zur Beschreibung der Stärke eines magnetischen Feldes geeignet ist. \(B\) bezeichnet die magnetische Flussdichte. Da die mag. Flussdichte \(B\) ein Maß für die Stärke des Magnetfeldes ist, sagt man kurz oft einfach nur das Magnetfeld \(B\).
Definition: Magnetfeld (magnetische Flussdichte) \(B\)
\[B = \frac{F_{\rm{m}}}{{{I_{\rm{L}}} \cdot l}}\]
\[{\left[ B \right] = \frac{{\left[ {{F_{\rm{m}}}} \right]}}{{\left[ {{I_{\rm{L}}}} \right] \cdot \left[ l \right]}} = 1\frac{{\rm{N}}}{{{\rm{A}} \cdot {\rm{m}}}} = 1\frac{{{\rm{N}} \cdot {\rm{m}}}}{{{\rm{A}} \cdot {{\rm{m}}^2}}} = 1\frac{{\rm{J}}}{{{\rm{A}} \cdot {{\rm{m}}^2}}} = 1\frac{{{\rm{V}} \cdot {\rm{A}} \cdot {\rm{s}}}}{{{\rm{A}} \cdot {{\rm{m}}^2}}} = 1\frac{{{\rm{V}} \cdot {\rm{s}}}}{{{{\rm{m}}^2}}}}\]
Hinweis: Zur Erinnerung an den großen Physiker Nicolas TESLA bezeichnet man die Einheit der magnetischen Flussdichte häufig als 1 Tesla (\(1\rm{T}\)): \(1\frac{{{\rm{V}} \cdot {\rm{s}}}}{{{{\rm{m}}^2}}} = 1{\rm{T}}\)
Verständnisaufgabe
Aufgabe
Bestimme für diesen Versuch die Stärke \(B\) des Magnetfeldes in der Feldspule.