Für manche Experimente benötigt man ein annähernd homogenes Magnetfeld, wie es in einer Zylinderspule gegeben ist. Zusätzlich soll dabei der Raum des homogenen Magnetfeldes ungestört von außen beobachtbar sein. Da bei der Zylinderspule die Windungen den seitlichen Blick auf den homogenen Feldbereich verwehren, erdachte der deutsche Physik Hermann von HELMHOLTZ (1821–1894) eine Anordnung, welche dieses Problem löst.
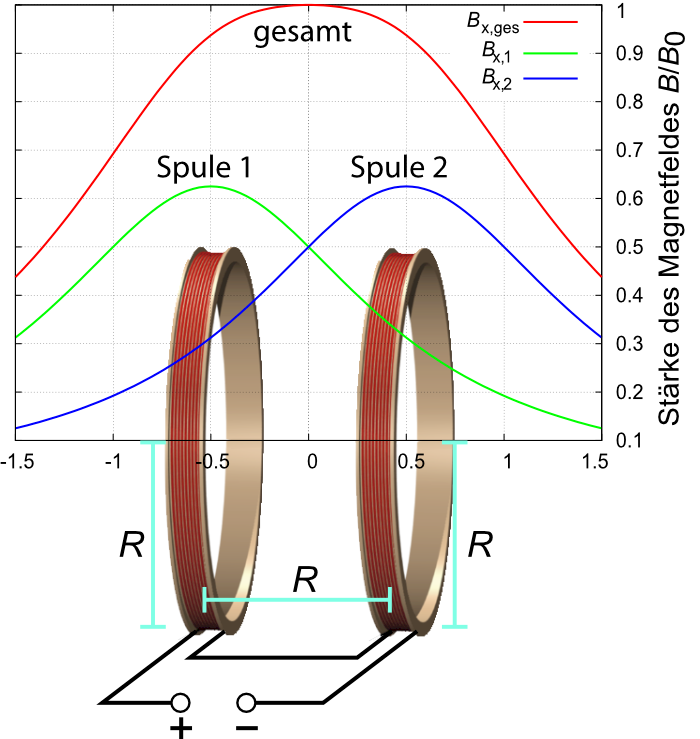
HELMHOLTZ stellte zwei flache, kreisförmige Spulen mit dem Radius \(R\) im Abstand \(R\) auf (vgl. Abb. 1). Dadurch entsteht in der Mittelebene des Spulenpaars ein annähernd homogenes Magnetfeld.
In Abb. 1 ist der Feldverlauf in \(x\)-Richtung der Einzelspulen und der resultierende Feldverlauf dargestellt. Der Vorteil von HELMHOLTZ-Spulen ist, dass man ein Experiment, welches zwischen den Spulen aufgebaut ist, ungehindert von außen beobachten kann.
Magnetfeld einer HELMHOLTZ-Spule
Haben die beiden Spulen einer HELMHOLTZ-Spule jeweils die Windungszahl \(N\), sowohl den Radius \(R\) als auch den Spulenabstand \(R\) und fließt durch das Spulenpaar ein Strom der Stärke \(I\), so berechnet sich der Betrag \(B\) der magnetischen Flussdichte in der Mittelebene der beiden Spulen durch\[B = {\mu_0} \cdot \frac{{8 \cdot N}}{{{{\sqrt {125} }} \cdot R}} \cdot I\] mit der magnetischen Feldkonstanten \(\mu_0=1{,}2566\cdot 10^{-6}\,\rm{\frac{N}{A^2}}\).