Hypothesen
Es liegt die Vermutung nahe, dass der Widerstand eines Drahtes sowohl von seinen Geometrie-Größen als auch von seinem Material abhängt. Daher müssen die folgenden Parameter auf den Einfluss des Widerstandes untersucht werden:
- Länge des Drahtes
- Querschnittsfläche des Drahtes
- Material des Drahtes
Mit den Ergebnissen der Teilversuche kann anschließend der spezifische Widerstand eingeführt und festgelegt werden.
Abhängigkeit des Widerstands eines Drahtes von seiner Länge
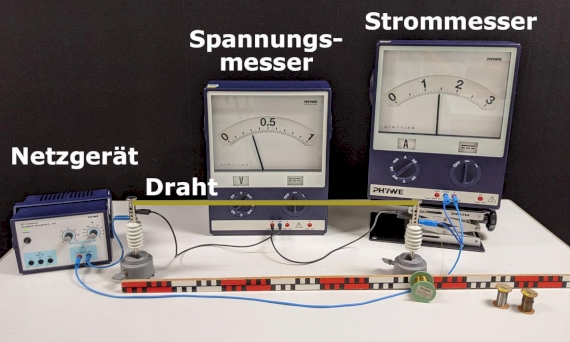
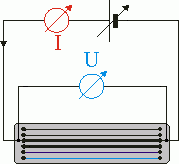
Um die Abhängigkeit des Widerstandswertes von der Drahtlänge zu untersuchen wählen wir die spannungsrichtige Schaltung. Hierbei macht man bei der Strommessung zwar einen kleinen Fehler, dieser fällt jedoch nicht ins Gewicht, da der Hauptteil des Stromes durch den niederohmigen Draht fließt und nur ein zu vernachlässigender Anteil durch den hochohmigen Spannungsmesser.

Aufgabe
Bei dem verwendeten Chrom-Nickel-Draht mit \({A = 0{,}20\,{{\rm{mm}}^2}}\) ergaben sich bei der Variation der Drahtlänge die folgenden Messwerte:
| Drahtlänge \({l\;{\rm{in}}\;{\rm{m}}}\) | \(0{,}25\) | \(0{,}50\) | \(0{,}75\) | \(1{,}00\) |
|---|---|---|---|---|
| Stromstärke \(I\;{\rm{in}}\;{\rm{A}}\) | \(1{,}0\) | \(1{,}0\) | \(1{,}0\) | \(1{,}0\) |
| Spannung \(U{\rm{\;in\;V}}\) | \(1{,}3\) | \(2{,}7\) | \(4{,}0\) | \(5{,}3\) |
Ergänze die Tabelle so, dass man die direkte Proportionalität zwischen Widerstandswert und Drahtlänge unmittelbar sieht.
Abhängigkeit des Widerstands eines Drahtes von seiner Querschnittsfläche
Um die Abhängigkeit des Widerstandswertes von der Querschnittsfläche zu untersuchen wählen wir wiederum die spannungsrichtige Schaltung. Auf einem Brett befinden sich mehrere Drähte (Widerstandsbrett) gleicher Länge, aber verschiedener Querschnittsfläche aus Konstantan.

Aufgabe
Bei dem verwendeten Konstantan-Draht mit \(l = 1{,}00\,{\rm{m}}\) ergaben sich bei der Variation der Querschnittsfläche die folgenden Messwerte:
| Querschnittsfläche \({A\;{\rm{in}}\;{\rm{mm^2}}}\) | \(0{,}10\) | \(0{,}20\) | \(0{,}30\) | \(0{,}40\) |
|---|---|---|---|---|
| Stromstärke \(I\;{\rm{in}}\;{\rm{A}}\) | \(0{,}27\) | \(0{,}54\) | \(0{,}76\) | \(1{,}0\) |
| Spannung \(U{\rm{\;in\;V}}\) | \(1{,}5\) | \(1{,}5\) | \(1{,}5\) | \(1{,}5\) |
Berechne aus den obigen Versuchsdaten den spezifischen Widerstand der drei Materialien in \(\frac{{\Omega \cdot {\rm{m}}{{\rm{m}}^2}}}{{\rm{m}}}\;{\rm{bzw}}{\rm{.}}\;\;\Omega \cdot {\rm{m}}\).
Die Längen- und Querschnittsabhängigkeit des Widerstandswertes eines Drahtes können nun zusammengefasst werden:
Aus \(R \sim l\) (bei gleichem Material und gleicher Querschnittsfläche) und \(R \sim \frac{1}{A}\) (bei gleichem Material und gleicher Drahtlänge) kann man schließen \(R \sim \frac{l}{A}\).
Spezifischer Widerstand als Proportionalitätskonstante
Um von der Proportionalitätsaussage zu einer Gleichung zu gelangen, führt man eine Proportionalitätskonstante \(\rho \) (gesprochen: "rho"), den sogenannten spezifischen Widerstand ein, in deren Größe auch die Eigenschaften des verwendeten Drahtmaterials einfließen. Damit ergibt sich
\[R = \rho \cdot \frac{l}{A}\]
Für die Einheit des spezifischen Widerstandes \(\rho \) erhält man wegen \(R = \rho \cdot \frac{l}{A} \Leftrightarrow \rho = \frac{{R \cdot A}}{l}\): \(\left[ \rho \right] = \frac{{\Omega \cdot {\rm{m}}{{\rm{m}}^{\rm{2}}}}}{{\rm{m}}}\).
Aufgabe
In einem dritten Versuch wird der Widerstand von Drähten gleicher Länge (\(l = 1,00{\rm{m}}\)) und Querschnittsfläche (\({A = 0,20{\rm{m}}{{\rm{m}}^2}}\)), aber aus unterschiedlichen Materialien untersucht:
| Material | Konstantan | Chrom-Nickel | Messing |
|---|---|---|---|
| Stromstärke \(I\;{\rm{in}}\;{\rm{A}}\) | \(0{,}54\) | \(0{,}50\) | \(0{,}85\) |
| Spannung \(U{\rm{\;in\;V}}\) | \(1{,}5\) | \(2{,}7\) | \(0{,}30\) |
Berechne die spezifischen Widerstände von Konstantan, Chrom-Nickel und Messing aus den Werten in der Tabelle.

