Versuch mit der elektrischen Feinwaage
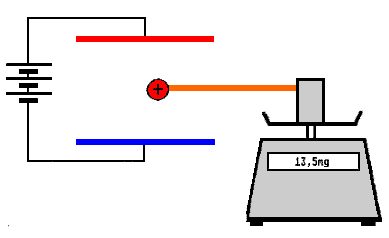

An einer elektrischen Feinwaage wird ein "Elektrostatik- Löffel" (kreisrunde Metallplatte mit Isolierstiel) befestigt. Dieser wird ins Innere eines Plattenkondensators gebracht und die elektrische Kraft in Abhängigkeit von der auf dem Löffel befindlichen Ladung und der Spannung des Kondensators gemessen.
Teilversuch 1: Veränderung der Ladung auf dem Probelöffel bei konstanter Kondensatorspannung
Durchführung
•Der "Elektrostatik-Löffel" ist zunächst ungeladen (Berührung mit der Hand des Experimentators, der sich selbst zuvor durch Berühren mit der Wasserleitung geerdet hat); er wird in die Mitte zwischen die Platten des Kondensators gebracht.
•Dann wird eine Spannung von ca. \(15,0\rm{kV}\) angelegt und die Waage beobachtet. Zeigt die Waage keine Veränderung (Ausschlag bleibt gleich), so hat der "Elektrostatik-Löffel" die richtige Position. Verändert sich der Ausschlag der Waage, so halten sich die durch Influenz bedingten Kräfte von oberer und unterer Kondensatorplatte auf den Elektrostatiklöffel nicht die Waage. Dies kann daran liegen, dass die metallische Fläche des Löffels nicht parallel zu den Kondensatorplatten ist oder dass sich der Löffel nicht in der Mitte zwischen den Kondensatorplatten befindet. Nach geometrischen Korrekturen sollte auf den ungeladenen Löffel im geladenen Kondensator keine nennenswerte Kraft ausgeübt werden.
•Nun lädt man den Löffel positiv auf. Die erreicht man z.B. indem man ihn kurzzeitig leitend mit der oberen Platte verbindet. Dadurch kommt es zu einer elektrischen Kraft nach unten. Man liest die Zunahme des Ausschlages der Waage ab (Anzeige in \(\rm{g}\) oder \(\rm{mg}\)) und rechnet ihn in Krafteinheiten (\(\rm{N}\) oder \(\rm{mN}\)) um.
•Anschließend halbiert man die Ladung auf dem Löffel indem man ihn mit einem gleichartigen ungeladenen Löffel im feldfreien Raum berührt. Dazu dreht man am besten den geladenen Löffel aus dem Kondensator und bringt ihn mit dem gleichartigen ungeladenen Löffel in Kontakt (Man könnte die Ladungshalbierung auch innerhalb des Kondensators durchführen, jedoch muss dazu dann die Spannung am Kondensator abgeschaltet werden. Dies ist umständlicher und dauert länger).
•Anschließend dreht man den Elektrostatiklöffel auf dem die Ladung halbiert wurde wieder in den gleich geladenen Kondensator und misst die Kraft auf den Elektrostatiklöffel.
•Die obige Prozedur der Ladungshalbierung und Kraftmessung wird so oft wiederholt bis die Kraft auf den Probelöffel zu klein für eine sinnvolle Ablesung ist.
Beobachtung
| Ladung | \(Q\) | \(\frac{1}{2}Q\) | \(\frac{1}{4}Q\) |
| Kraft \({F_{{\rm{el}}}}\;{\rm{in}}\;{\rm{mN}}\) | \(22\) | \(11\) | \(6\) |
Auswertung
Zunächst könnte man auf die Idee kommen, die Kraft \({F_{{\rm{el}}}}\) auf den Probelöffel als Maß für die "Stärke" des elektrischen Feldes im Kondensator zu verwenden. Der Versuch zeigt jedoch, dass diese Kraft nicht nur vom elektrischen Feld des Kondensators, sondern ganz wesentlich auch von der Ladung \(Q\) auf der Sonde (Probelöffel) abhängt mit der das Feld untersucht wird. Die obige Messung zeigt nämlich \({F_{{\rm{el}}}} \sim Q\) bei gleichbleibendem elektrischen Feld.
Als feldbeschreibende Größe wählt man daher sinnvollerweise den Quotienten \(\frac{{{F_{{\rm{el}}}}}}{Q}\). Dieser Quotient ist bei gleichbleibendem Feld eine Konstante, da aus der Proportionalität von Kraft \({{F_{{\rm{el}}}}}\) und Löffelladung \(Q\) die Konstanz von \(\frac{{{F_{{\rm{el}}}}}}{Q}\). Dieser Quotient beschreibt eine nur vom Feld abhängige Größe, die man als Feldstärke \(E\) definiert. Da die Kraft \({{F_{{\rm{el}}}}}\) ein Vektor ist und die Ladung \(Q\) kein Vektor ist, muss \(E\) ein Vektor in Richtung (oder Gegenrichtung) der Kraft sein. Die Richtung der Feldstärke wird als die Richtung der Kraft auf eine positive Probeladung definiert (die Kraft auf eine negative Probeladung ist entgegen der Feldstärkerichtung). Wir erhalten also\[\vec E = \frac{{{{\vec F}_{el}}}}{Q}\quad \left[ E \right] = 1\frac{{\rm{N}}}{{{\rm{As}}}}\]
Bei dem oben beschriebenen Versuch war die maximale Probeladung \(Q=11 \cdot 10^{-8}\rm{As}\).
Berechne aus dieser Angabe und mit Hilfe obiger Tabelle die elektrische Feldstärke bei dem durchgeführten Versuch.
Teilversuch 2: Veränderung der Kondensatorspannung bei konstanter Ladung auf dem Probelöffel
Durchführung
•Die Durchführung erfolg analog zu Teilversuch 1.
Beobachtung
| Spannung \(U\;{\rm{in}}\;{\rm{kV}}\) | \(20\) | \(15\) | \(10\) | \(5\) |
| Kraft \({F_{{\rm{el}}}}\;{\rm{in}}\;{\rm{mN}}\) | \(29\) | \(22\) | \(14\) | \(7\) |
Erläutere, welche Information man aus diesen Versuchsergebnissen ableiten kann.
Versuch mit der Kompensationswaage
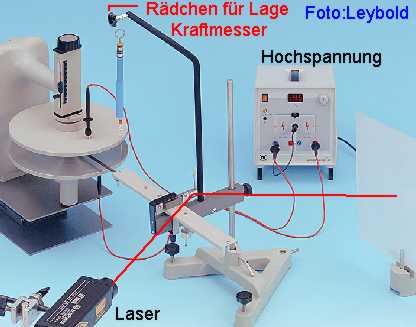
Aufbau und Durchführung
•An einen Arm einer sehr empfindlichen Balkenwaage wird ein Elektrostatiklöffel montiert. Dieser ragt in das Innere eines Plattenkondensators.
•Mit einem Lichtzeiger kann die Ausgangsstellung der Waage sehr genau kontrolliert werden.
•Wird der Kondensator und der Löffel geladen, so verändert dieser zunächst die Lage des Löffels.
•Mit einer Federwaage, die an dem Rädchen befestigt ist, wird der (linke) Waagbalken solange hoch gezogen, bis der Lichtzeiger wieder die Ausgangslage hat. In diesem Fall ist das durch die elektrische Kraft bewirkte Drehmoment und das durch die Federwaage bewirkte Drehmoment von gleichem Betrag.
•Mit Hilfe des Hebelgesetzes kann man nun die elektrische Kraft aus der Federkraft und den Hebelarmen berechnen. Kenn man die Ladung auf dem Elektrostatiklöffel, lässt sich dann die elektrische Feldstärke im Kondensator bestimmen.
Hinweis: Anstelle der Kompensationswaage kann auch ein elektronischer Kraftmesser eingesetzt werden.
Versuch mit der Drehwaage
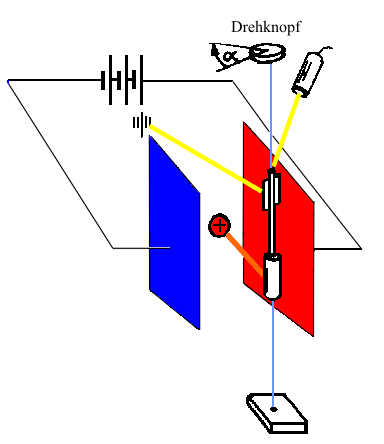
Aufbau und Durchführung
•Der Lichtzeiger kontrolliert die Ausgangsstellung der Drehwaage.
•Wird der Kondensator und die isoliert an einem Torsionsdraht befestigte Kugel geladen, so verändert die Kugel zunächst ihre Lage.
•Durch Drehen an dem oberen Knopf wird die Kugel mittels Torsionswirkung des Drahtes in die Ausgangslage zurück gebracht. Was sich mit dem Lichtzeiger leicht kontrollieren lässt
•Die Weite \(\alpha \) des Drehwinkels, um den man den Drehknopf dreht, ist wegen des Gesetzes von HOOHE zu dem bewirkten Drehmoment direkt proportional. Da die Hebelarme nicht verändert werden, ist die Winkelweite auch zur elektrischen Kraft auf die Kugelladung proportional.

