Arbeit des Feldes und Änderung der potentiellen Energie
Eine negative elektrische Ladung befindet sich im Punkt A im Inneren eines Plattenkondensators, der ein homogenes E-Feld erzeugt, und bewegt sich die Strecke \(s_{\rm{AB}}\) zum Punkt B (vgl. Animation in Abb. 1). Da hier die Kraftrichtung und die Wegrichtung bei der Bewegung des geladenen Körpers übereinstimmen, so verrichtet das elektrische Feld eine positiv zu zählende Feldarbeit\[{W_{{\rm{Feld}} \to {\rm{Körper}}}} = {F_{{\rm{el}}}} \cdot {s_{{\rm{AB}}}} = \left| q \right| \cdot \left| E \right| \cdot \left| {{s_{{\rm{AB}}}}} \right| > 0\]an der Ladung. Hinweis: Auf den rechten Seiten der obigen Gleichungen stehen jeweils Beträge.
Bei dem dargestellten Vorgang nimmt die potentielle Energie des geladenen Körpers gerade um den Betrag der Feldarbeit ab:\[\Delta {E_{\rm{pot}}} = - {W_{{\rm{Feld}} \to {\rm{Körper}}}} \Rightarrow \Delta {E_{\rm{pot,AB}}} = - \left| q \right| \cdot \left| E \right| \cdot \left| {{s_{\rm{AB}}}} \right| < 0 \quad(1)\]Achtung: Die obigen Aussagen beziehen sich auf den Spezialfall, bei dem die Richtung der elektrischen Kraft und die Richtung der Bewegung, also des Vektors \({\vec s_{\rm{AB}}}\) übereinstimmen. Sind die Richtung der elektrischen Kraft und die Richtung des Vektors \({\vec s_{\rm{AB}}}\) gerade entgegengesetzt, so ist die Feldarbeit negativ zu zählen und die potentielle Energie nimmt bei dem betrachteten Vorgang zu. In beiden Fällen gilt\[\Delta {E_{{\rm{pot}}}} = - {W_{{\rm{Feld}}}}\]
Festlegung eines Nullniveaus
In der Mechanik hat es sich bewährt, dass man für die potentielle Energie ein Nullniveau vereinbart. Ähnlich verfährt man auch im elektrischen Fall. Ordnen wir z.B. der negativ geladenen Platte die potentielle Energie Null zu, so gilt für die Bewegung einer positiven Probeladung von der negativen Platte aus, dass die potentielle Energie zunimmt, da die Bewegungsrichtung und die Kraftrichtung entgegengesetzt sind:\[{E_{{\rm{pot}}{\rm{,AB}}}} = {E_{{\rm{pot}}{\rm{,B}}}} - {E_{{\rm{pot}}{\rm{,A}}}} = \left| q \right| \cdot \left| E \right| \cdot \left| {{s_{{\rm{AB}}}}} \right|\]Da \({E_{{\rm{pot,A}}}} = 0\) gewählt wurde, gilt\[{E_{{\rm{pot,B}}}} = \left| q \right| \cdot \left| E \right| \cdot \left| {{s_{{\rm{AB}}}}} \right|\]Maximal wird die potentielle Energie der positiven Ladung, wenn man den Punkt B auf die positive Platte legt. Mit der Bezeichnung \(d\) für den Plattenabstand gilt so\[{E_{{\rm{pot,B}}}} = \left| q \right| \cdot \left| E \right| \cdot \left| d \right|\]
Detailliertere Betrachtungen unter Berücksichtigung der Richtung
Bei der Berechnung der Feldarbeit \({W_{{\rm{Feld}}}}\) muss man eigentlich berücksichtigen, dass sowohl die elektrische Kraft als auch der vom Ladungsträger zurückgelegte Weg Vektoren darstellen, die nicht nur in die gleiche oder die entgegengesetzte Richtung zeigen können, sondern in einem beliebigen Winkel \(\alpha\) zueinander stehen können. Die Feldarbeit ergibt sich dann als das Skalarprodukt des Vektors der Feldkraft \({\vec F_{\rm{el}}}\) und des Verschiebungsvektors \({\vec s_{\rm{AB}}}\). Damit gilt für die Feldarbeit\[{W_{\rm{Feld}}} = {\vec F_{\rm{el}}} \cdot {\vec s_{\rm{AB}}} = q \cdot \vec E \cdot {\vec s_{\rm{AB}}}\]Dabei ist \(q\) die Ladung des bewegten Körpers (kann positiv oder negativ sein), \(\vec E\) der Vektor der elektrischen Feldstärke, dessen Richtung mit der Kraftrichtung auf eine positive Probeladung zusammenfällt und \({\vec s_{\rm{AB}}}\) der Verschiebungsvektor, der die Richtung und die Länge der Ladungsverschiebung beinhaltet.
Mathematischer Exkurs: Skalarprodukt zweier Vektoren
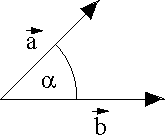
Als multiplikative Verknüpfung zweier Vektoren \(\vec a\) und \(\vec b\) kennt man in der Mathematik zwei Formen:
Das Vektorprodukt mit der Schreibweise \(\vec c = \vec a \times \vec b\). Das Ergebnis ist wiederum ein Vektor \(\vec c\), der auf der durch \(\vec a\) und \(\vec b\) aufgespannten Ebene senkrecht steht. Auf Einzelheiten dieser Produktform wird zunächst nicht eingegangen.
Das Skalarprodukt mit der Schreibweise \(d = \vec a \cdot \vec b\). Das Ergebnis ist eine skalare (nicht vektorielle) Größe \(d\). Die Vorschrift zur Berechnung des Skalars \(d\) lautet\[d = \left| {\vec a} \right| \cdot \left| {\vec b} \right| \cdot \cos \alpha \]Dabei bedeutet \(a = \left| {\vec a} \right|\) die Länge des Vektors \(\vec a\), \(b = \left| {\vec b} \right|\) die Länge des Vektors \(\vec b\) und \(\alpha \) den Winkel zwischen den beiden Vektoren \(\vec a\) und \(\vec b\).
Damit lautet die allgemeine Schreibweise für die Feldarbeit \({W_{{\rm{Feld}}}}\) bzw. die Änderung der potentiellen Energie \(\Delta {E_{{\rm{pot}}}}\) im homogenen elektrischen Feld\[{W_{\rm{Feld}}} = q \cdot \left| {\vec E} \right| \cdot \left| {{{\vec s}_{\rm{AB}}}} \right| \cdot \cos \left( \alpha \right) \]Da die Änderung der potentiellen Energie gleich dem Negativen der Feldarbeit ist (\(\Delta {E_{{\rm{pot}}}} = - {W_{{\rm{Feld}}}}\)), ergibt sich für \(\Delta {E_{{\rm{pot}}}}\)\[\Delta {E_{\rm{pot}}} = - q \cdot \left| {\vec E} \right| \cdot \left| {{{\vec s}_{\rm{AB}}}} \right| \cdot \cos \left( \alpha \right) \quad (2)\]
Anwendung auf einfache, aber wichtige Sonderfälle
Meist wenden wir die Beziehung \(\left(2\right)\) auf drei besonders einfache Sonderfälle an:
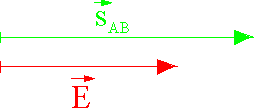
\(\vec E\) und \(\vec s_{\rm{AB}}\) haben die gleiche Orientierung: Dann ist \(\alpha = 0^\circ\), \(\cos \alpha = 1\) und \(\Delta {E_{\rm{pot}}} = - q \cdot \left| {\vec E} \right| \cdot \left| {{{\vec s}_{\rm{AB}}}} \right|\)
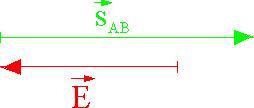
\(\vec E\) und \(\vec s_{\rm{AB}}\) haben entgegengesetze Orientierung: Dann ist \(\alpha = 180^\circ\), \(\cos \alpha = -1\) und \(\Delta {E_{\rm{pot}}} = (+) q \cdot \left| {\vec E} \right| \cdot \left| {{{\vec s}_{\rm{AB}}}} \right|\)
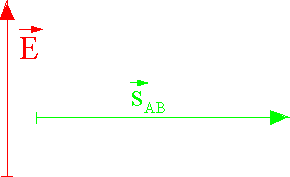
\(\vec E\) und \(\vec s_{\rm{AB}}\) stehen aufeinander senkrecht: Dann ist \(\alpha = 90^\circ\), \(\cos \alpha = 0\) und \(\Delta {E_{\rm{pot}}} =0\). Stehen also \(\vec E\) und \({\vec s_{\rm{AB}}}\) aufeinander senkrecht, so wird keine Feldarbeit verrichtet. Bei der Bewegung des Ladungsträgers ändert sich dessen potentielle Energie nicht

