 Joachim Herz Stiftung
Joachim Herz Stiftung
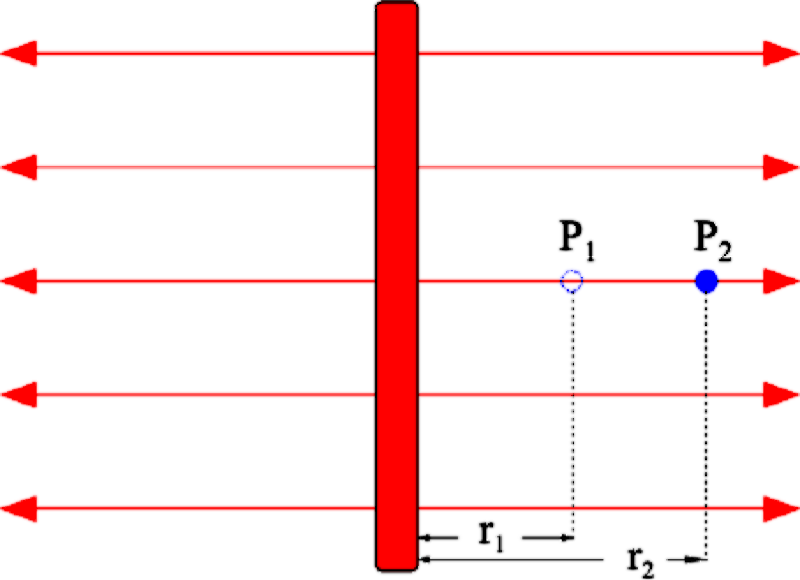
Abb. 1 VersuchsaufbauEin negativ aufgeladener Probekörper (\({q_1}=-1{,}0 \cdot {10^{ - 9}}{\rm{As}}\) wird im homogenen elektrischen Feld (\(E = 2{,}0 \cdot {10^2}\,\frac{{\rm{N}}}{{{\rm{As}}}}\)) einer positiv geladenen Platte von P1 (\({r_1} = 4{,}0\,{\rm{cm}}\)) nach P2 (\({r_2} = 7{,}0\,{\rm{cm}}\)) gebracht.