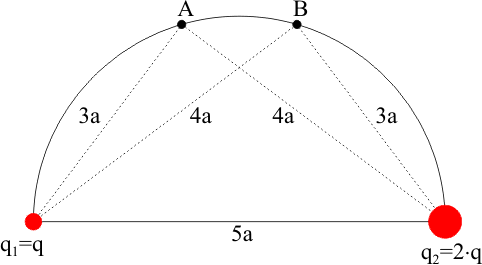
Wie in nebenstehender Skizze gezeichnet, stehen sich zwei Ladungen q1 = q und q2 =2·q in der gegenseitigen Entfernung 5a gegenüber.
a)Berechnen Sie die resultierende Feldstärke \(\left| {{{\vec E}_A}} \right|\) im Punkt A.
b)Bestimmen Sie zeichnerisch die Richtung von \({\vec E}_A \).
c)Welche Potentialdifferenz ΔφAB misst man zwischen den Punkten A und B?