Ladungen & Felder - Mittelstufe

Grundwissen

Ladung und Strom - Fortführung

Das Wichtigste auf einen Blick

Die Fläche im Zeit-Stromstärke-Diagramm entspricht der geflossenen Ladungsmenge \(\Delta Q\).
Somit kann auch die geflossene Ladungsmenge bei variabler Stromstärke \(I\) ermittelt werden.

Verallgemeinerung des Zusammenhangs zwischen Strom und Ladung

**Abb. 1** Zusammenhang von Ladung und Strom bei konstantem Stromfluss

Liegt bei einem Vorgang in der Elektrizitätslehre ein konstanter Strom der Stärke \(I\) vor, so lässt sich die in eine Zeitspanne \(\Delta t\) geflossene Ladung \(\Delta Q\) wie bereits bekannt nach der Beziehung\[\Delta Q = I \cdot \Delta t\]berechnen. Wie die Skizze in Abb. 1 zeigt, ist die Fläche unter dem \(t\)-\(I\)-Graphen ein Maß für die geflossene Ladung.

Näherung bei nicht konstantem Stromfluss

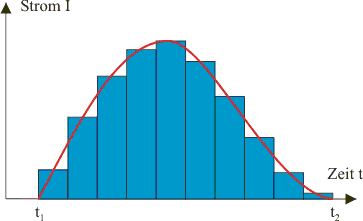
Abb. 2 Bestimmung der geflossenen Ladungsmenge durch die Flächenbestimmung im Zeit-Stromstärke-Diagramm

Liegt kein zeitlich konstanter Verlauf der Stromstärke vor (Abb. 2), so kann man die oben erworbenen Kenntnisse gewinnbringend für eine näherungsweise Bestimmung der Ladung verwenden. Auch bei variablem Stromverlauf deutet man die Fläche unter dem \(t\)-\(I\)-Graphen als Maß für die geflossene Ladung. Da uns mathematisch noch kein Handwerkszeug zur Verfügung steht, um die Fläche unter der nebenstehenden Zeit-Strom-Kurve zu bestimmen, nähern wir die krummlinig begrenzte Fläche durch Rechtecksflächen an. Dies Annäherung wird um so genauer je kleiner die Breite \(\Delta t'\) der Rechtecke wird. Für eine möglichst genau Annäherung müsste \(\Delta t'\) gegen Null streben. Dies wird in der Animation veranschaulicht.

Zusammenfassung der Beziehungen zwischen Stromstärke und Ladung

konstante Stromstärke

zeitlich variable Stromstärke

\[I = \frac{{\Delta Q}}{{\Delta t}}\]

\[\Delta Q = I \cdot \Delta t\]

\[I = \frac{{dQ}}{{dt}}\]

\[\Delta Q \approx {I_1} \cdot \Delta t + {I_2} \cdot \Delta t + {I_3} \cdot \Delta t + \;.\;.\;.\] oder mit Hilfe der Integrationsrechnung, welche du evtl. erst noch lernen wirst \[\Delta Q = \int\limits_{{t_1}}^{{t_2}} {I(t)dt} \]

Die Elementarladung

Abb. 5 Robert Andrews Millikan (1868-1953)

Bei einfachen Versuchen in der Schule könnte man den Eindruck gewinnen, dass elektrische Ladung in beliebigen Mengen verfügbar, d.h. die elektrische Ladung eine kontinuierlich veränderbare Größe ist. Geht man jedoch zu sehr kleinen Ladungswerten, so stellt man fest (R. Millikan 1909), dass sich die Ladungswerte "stufenartig" ändern und sich jeder Ladungswert als Vielfaches einer bestimmten kleinsten Ladung, der Elementarladung darstellen lässt.

Millikan bestimmte den Wert dieser Elementarladung e mit einer sehr ausgeklügelten Anordnung. Im Jahr 1923 bekam er dafür den Nobelpreis. Er erhielt den folgenden, für uns unvorstellbar kleinen, Wert für \(e\):\[e=1{,}6022\cdot 10^{-19}\,\rm{As}\]

Ein Elektron trägt die Ladung \(q_{\rm{Elektron}}=-e\). Das Proton, der positiv geladene Baustein von Atomkernen trägt die Ladung \(q_{\rm{Elektron}}=+e\).

Hinweis: Bis vor kurzem war man der Auffassung, dass die Elementarladung die kleinste vorkommende Ladungsportion ist. Neuere Theorien vom Aufbau der Materie gehen jedoch davon aus, dass z.B. das Proton aus noch kleineren Teilchen, den sogenannten Quarks besteht. Bei den Quarks gibt es Teilchen, die als Ladung nur einen Bruchteil von \(e\) tragen.

Elektronenfluss durch einen Leiterquerschnitt

Mit Hilfe der Elementarladung sind wir nun z.B. in der Lage auszurechnen, wie viele Elektron in 1,0 Sekunden durch einen Leiterquerschnitt fließen, wenn die Stromstärke z.B. 1,0 A beträgt. Für den Strom gilt:
\[I = \frac{{\Delta Q}}{{\Delta t}}\]
Die durch den Leiterquerschnitt in einer bestimmten Zeit geflossene Ladung setzt sich aus der Zahl N von Elektronen mit dem Ladungsbetrag e zusammen. Somit gilt:
\[I = \frac{{N \cdot e}}{{\Delta t}}\quad \Rightarrow \quad N = \frac{{I \cdot \Delta t}}{e}\quad \Rightarrow \quad N \approx \frac{{1,0 \cdot 1,0}}{{1,6 \cdot {{10}^{ - 19}}}}\frac{{{\rm{A}} \cdot {\rm{s}}}}{{{\rm{A}} \cdot {\rm{s}}}} = 6,3 \cdot {10^{18}}\]
Diese große Zahl lässt verstehen, dass wir in der Praxis den Strom nicht dadurch messen werden, dass wir Elektronen zählen, die in einer bestimmten Zeit durch einen Leiterquerschnitt treten. Darüber hinaus würde diese Methode voraussetzen, dass wir einzelne Elektronen "sehen" könnten.

Drucken