Versuchsaufbau
Eine Feldspule wird mit einer steuerbaren Stromquelle betrieben, die dafür sorgt, dass der Strom in der Feldspule zeitlich linear ansteigt und abfällt. Der Stromverlauf wird mit einem Amperemeter dargestellt und die Zeit des Spannungsanstieges muss gemessen werden.
In der Feldspule befindet sich wie in Abb. 2 skizziert eine Induktionsspule. Die in dieser Spule entstehende Induktionsspannung \(U_{\rm{ind}}\) wird mit einem mV-Messgerät nachgewiesen.
Alternativen: Anstelle der steuerbaren Stromquelle kann natürlich auch ein leistungsstarker Funktionsgenerator (Ausgangsstrom mind. 0,5 A) genutzt werden. Die Messung des Stroms in der Feldspule und der Induktionsspannung kann auch mittels digitalem Messwerterfassungssystem erfolgen. Dann ist eine analoge Zeitmessung nicht mehr erforderlich.
Versuchsdurchführung und Ergebnis
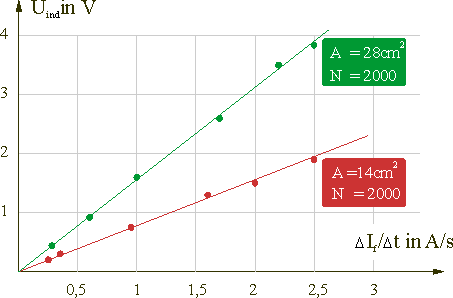
a) Untersuchung des Zusammenhangs zwischen Uind und ΔB/Δt und A:
1. Versuch:
Es wird die Zeit T, in welcher der Strom in der Feldspule von Null auf seinen Maximalwert (If,max) ansteigt, variiert:
Spulendaten: Querschnittsfläche A= 14cm2; Windungszahl N = 2000
Maximaler Feldstrom If,max= 6,0A
|
T in s
|
25,5
|
16,5
|
6,2
|
3,5
|
3,0
|
2,4
|
|
Uind in V
|
0,18
|
0,27
|
0,74
|
1,3
|
1,5
|
1,9
|
Während des zeitlich linearen Stromanstiegs stellt sich jeweils ein konstanter Wert der Induktionsspannung ein.
2. Versuch:
In einem zweiten Versuch wird die erste Induktionsspule gegen eine zweite mit doppelter Querschnittsfläche und gleicher Windungszahl ausgetauscht:
Spulendaten: Querschnittsfläche A = 28cm2; Windungszahl N = 2000
Maximaler Feldstrom If,max= 6,0A
|
T in s
|
24,3
|
10,2
|
5,9
|
3,5
|
2,7
|
2,4
|
|
Uind in V
|
0,39
|
0,93
|
1,6
|
2,7
|
3,5
|
3,9
|
Während des zeitlich linearen Stromanstiegs stellt sich jeweils ein konstanter Wert der Induktionsspannung ein.
Erläutere, welche Schlussfolgerungen man aus diesen beiden Versuchen ziehen kann. Stelle deine Überlegungen - auch unter Benutzung einer Grafik - sauber dar.
Zeige, dass durch die beiden Versuche die Beziehung \({U_{ind}} \sim A \cdot \frac{{\Delta B}}{{\Delta t}}\) bestätigt werden kann.
Als Ergebnis der beiden ersten Versuche kann man festhalten:
\[{U_{ind}} \sim A \cdot \frac{{\Delta B}}{{\Delta t}}\quad \left( 3 \right)\]
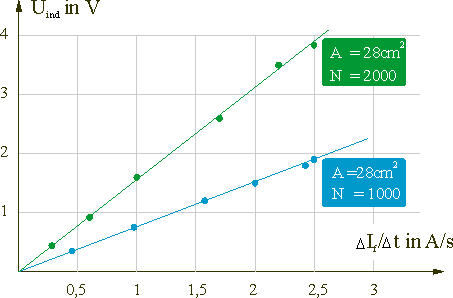
b) Untersuchung des Zusammenhangs zwischen Uind und N:
3. Versuch:
In einer dritten Versuchsreihe wird eine Spule verwendet deren Querschnittsfläche mit der Spule der zweiten Messreihe übereinstimmt, deren Windungszahl jedoch nur halb so groß ist.
Spulendaten: Querschnittsfläche A = 28cm2; Windungszahl N = 1000; Maximalstrom Imax= 6,0A
|
T in s
|
14,4
|
6,3
|
4,2
|
3,0
|
2,5
|
2,4
|
|
Uind in V
|
0,32
|
0,73
|
1,2
|
1,5
|
1,8
|
1,9
|
Erläutere, welche Schlussfolgerungen man aus dem Vergleich des 2. und 3. Versuchs ziehen kann. Stelle deine Überlegungen - auch unter Benutzung einer Grafik - sauber dar.
Als Ergebnis des dritten Versuchs kann man festhalten:
\[{U_{ind}} \sim {\rm N}\quad \left( 4 \right)\]
Kombiniert man die Proportionalitäten (3) und (4), so ergibt sich:
\[{U_{ind}} \sim {\rm N} \cdot {\rm A} \cdot \frac{{\Delta B}}{{\Delta t}}\]
-
Die genaue Auswertung des Versuchs (oder abereine kompliziertere theoretische Überlegung mit Hilfe der MAXWELL-Gleichungen) zeigt, dass der Proportionalitätsfaktor in obiger Beziehung den Wert 1 hat.
-
Wie später gezeigt wird (Selbstinduktion), ist es angebracht in die Gleichung ein Minuszeichen einzuführen. Somit ergibt sich:
|
Induktionsgesetz in differentieller Form \[{U_{ind}} = - {\rm N} \cdot {\rm A} \cdot \frac{{\Delta B}}{{\Delta t}}\] |