Material und Versuchsaufbau
Benötigte Geräte
- Elektromagnet mit Polschuhen
- Gleichstromquelle und Strommesser für den Spulenstrom (mind. \(5\,{\rm{A}}\))
- Hallapparat mit Silberblech
- Gleichstromquelle mit Strommesser für den Querstrom (mind. \(20\,{\rm{A}}\))
- Messverstärker zur Messung der HALL-Spannung
- Multimeter zur Anzeige der HALL-Spannung
Kalibrieren des Elektromagneten (vgl. Link am Ende dieses Artikels)
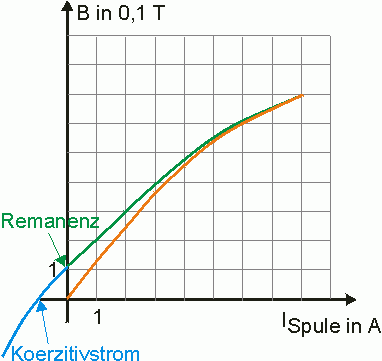
Um die Abhängigkeit der HALL-Spannung von der magnetischen Feldstärke \(B\) zu untersuchen, müsste man während des Versuchs die magnetische Flussdichte messen können. Dazu müsste man aber jeweils die HALL-Apparatur aus dem Elektromagneten herausnehmen, was praktisch nicht möglich ist. Deshalb erstellt man vor der eigentlichen Versuchsdurchführung eine "Kalibrierkurve", die die magnetische Feldstärke in Abhängigkeit vom Spulenstrom darstellt. Als Ergebnis erhält man z.B. die folgende Kalibrierkurve:
Die orange Kurve ist für den Versuch zu verwenden, man nennt sie "Neukurve", weil der Eisenkern anfangs unmagnetisch (neu) ist. Man erkennt den Restmagnetismus (Remanenz) und den nötigen Gegenstrom (Koerzitivstrom).
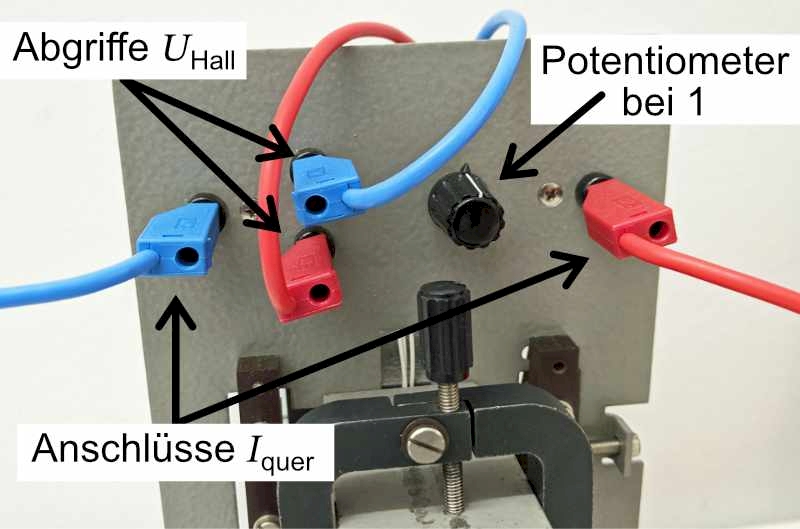
Justieren der Abgriffe für die HALL-Spannung
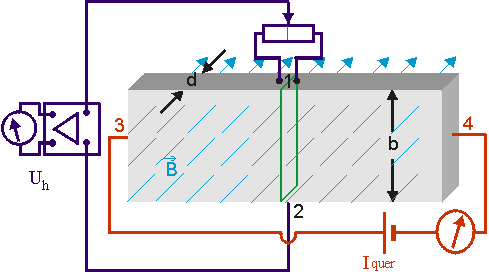
An die Punkte 3 und 4 wird eine Spannung von ca. \(30\,\rm{V}\) gelegt, damit der Querstrom \(I_{\rm{quer}}\) fließt. Dadurch entsteht im Hallplättchen von links nach rechts ein von der Stärke des Querstroms abhängiges Potentialgefälle. Damit man zwischen den beiden Abgriffen 1 und 2 die HALL-Spannung und nicht das Potentialgefälle misst, müssen sie auf einer Äquipotentialfläche (grün) angebracht sein.
Dies erreicht man, indem man zunächst ohne Strom und Magnetfeld den Nullpunkt des spannungsempfindlichen Messverstärkers justiert, dann noch ohne Magnetfeld den Querstrom hochregelt. Meist stellt man jetzt schon am Messverstärker eine Spannung fest, obwohl noch gar kein Halleffekt auftreten kann, da \(B = 0\) ist. Man kompensiert die nachgewiesene Spannung durch das bei 1 angebrachte Potentiometer, an dem man so lange dreht, bis am Messverstärker die Spannung Null angezeigt wird.
Abhängigkeit der HALL-Spannung von der Stärke des Magnetfeldes \(B\)
Man lässt den Querstrom \(I_{\rm{quer}}\) während des gesamten Teilversuchs konstant durch das Silberplättchen fließen und erhöht langsam in Schritten von \(1\,\rm{A}\) den Spulenstrom und damit das Magnetfeld. Dabei ist darauf zu achten, dass zu Beginn der Restmagnetismus abgebaut wurde und dass man während des Versuchs den Strom nur steigern, nicht mindern darf. Für \(I_{\rm{quer}} = 15{,}0\,\rm{A}\) erhält man:
| \(I_{\rm{sp}}\) in \(\rm{A}\) | 1,0 | 2,0 | 3,0 | 4,0 | 6,0 | 8,0 |
|---|---|---|---|---|---|---|
| \(B\) in \(\rm{\frac{Vs}{m^2}}\) | 0,13 | 0,25 | 0,36 | 0,46 | 0,59 | 0,69 |
| \(U_{\rm{H}}\) in \(10^{-6}\rm{V}\) | 2,2 | 4,8 | 7,5 | 9,0 | 11,9 | 13,6 |
Aufgabe
Fertige ein \(B\)-\(U_{\rm{H}}\)-Diagramm an und werte dieses aus.
Abhängigkeit der HALL-Spannung vom Querstrom
Man lässt den Spulenstrom und damit das Magnetfeld während des gesamten Teilversuchs konstant und variiert den Querstrom \(I_{\rm{quer}}\).
| \(I_{\rm{quer}}\) in \(\rm{A}\) | 4,0 | 8,0 | 12,0 | 16,0 |
|---|---|---|---|---|
| \(U_{\rm{H}}\) in \(10^{-6}\rm{V}\) | 4,4 | 9,0 | 12,6 | 16,4 |
Aufgabe
Fertige ein \(U_{\rm{H}}\)-\(I_{\rm{quer}}\)-Diagramm an und werte dieses aus.
Theorie
Annahmen
- Es gibt nur eine Sorte von beweglichen Ladungsträgern (z.B. Elektronen) die zum Strom beitragen.
- Alle Ladungsträger queren mit der gleichen Geschwindigkeit \(v\) das Silberband.
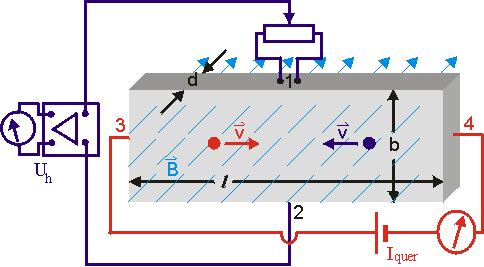
Durch das Magnetfeld wirkt eine Lorentzkraft vom Betrag \({F_{\rm{L}}} = q \cdot v \cdot B\), welche die Ladungsträger nach oben zum Anschluss 1 verschiebt. Diese Verschiebungsrichtung zum Anschluss 1 wäre für positive und negative Ladungsträger dieselbe.
Die Verschiebung geht so lange, bis das durch die Ladungsverschiebung aufgebaute elektrische Feld eine der Lorentzkraft entgegengesetzt gerichtete und betraglich gleichgroße elektrische Kraft mit dem Betrag \({F_{{\rm{el}}}} = q \cdot \frac{{{U_{\rm{H}}}}}{b}\) bewirkt:\[{F_{\rm{L}}} = {F_{{\rm{el}}}} \quad \Leftrightarrow \quad q \cdot v \cdot B = q \cdot \frac{{{U_{\rm{H}}}}}{b} \quad \Leftrightarrow \quad {\kern 1pt} {U_{\rm{H}}} = b \cdot v \cdot B\]Dies wird durch den Versuch (\({U_{\rm{H}}} \sim B\)) bestätigt.
Die Zahl der im gesamten Silberband befindlichen freien Ladungsträger ist \(N\). Die Zeit während ein Ladungsträger die Länge \(l\) des Silberbands durchquert ist \(t\). Während dieser Zeit \(t\) werden alle \(N\) freien Ladungsträger im Silberband ausgetauscht und während dieser Zeit \(t\) bewegen sich genau \(N\) freie Ladungsträger durch einen Leiterquerschnitt. Für den Strom \({I_{{\rm{quer}}}}\) gilt dann\[{I_{{\rm{quer}}}} = \frac{{N \cdot q}}{t} \quad \Leftrightarrow \quad t = \frac{{N \cdot q}}{{{I_{{\rm{quer}}}}}}\]In die Gleichung für die Geschwindigkeit eingesetzt ergibt sich\[v = \frac{l}{t} = \frac{{l \cdot {I_{{\rm{quer}}}}}}{{N \cdot q}}\]In die Gleichung für die Hallspannung eingesetzt ergibt sich\[{U_{\rm{H}}} = b \cdot \frac{{l \cdot {I_{{\rm{quer}}}}}}{{N \cdot q}} \cdot B\]Dies wird durch den Versuch (\({U_{\rm{H}}} \sim {I_{{\rm{quer}}}}\)) bestätigt.
Weitere Umformungen (Erweitern mit \(d\) und Einsetzen des Volumens \(V = b \cdot l \cdot d\)) führen zu\[\begin{eqnarray}{U_{\rm{H}}} &=& b \cdot \frac{{l \cdot {I_{{\rm{quer}}}}}}{{N \cdot q}} \cdot B\\ &=& \frac{{b \cdot l \cdot d}}{{N \cdot q}} \cdot \frac{{{I_{{\rm{quer}}}} \cdot B}}{d}\\ &=& \frac{V}{{N \cdot q}} \cdot \frac{{{I_{{\rm{quer}}}} \cdot B}}{d}\\ &=& \frac{1}{{n \cdot q}} \cdot \frac{{{I_{{\rm{quer}}}} \cdot B}}{d}\\ &=& {R_{\rm{H}}} \cdot \frac{{{I_{{\rm{quer}}}} \cdot B}}{d}\end{eqnarray}\]Dabei ist \({n = \frac{N}{V}}\) die Ladungsträgerdichte und \({{R_{\rm{H}}} = \frac{1}{{n \cdot q}}}\) die Hallkonstante des Materials.