HALL-Effekt / HALL-Spannung / HALL-Konstante
Befindet sich ein stromdurchflossener Leiter in einem homogenen Magnetfeld, dann baut sich senkrecht sowohl zur Stromfluss- als auch zur Magnetfeldrichtung über dem Leiter eine Spannung auf. Diesen Effekt bezeichnet man als HALL-Effekt, die aufgebaute Spannung als HALL-Spannung \(U_{\rm{H}}\).
Ist \(I\) die Stärke des Stroms durch den Leiter, \(B\) die magnetische Feldstärke und \(d\) die Dicke des Leiters parallel zu \(\vec B\), dann berechnet sich die HALL-Spannung durch\[{U_{\rm{H}}} = {R_{\rm{H}}} \cdot \frac{{I \cdot B}}{d}\]mit der vom Material des Leiters abhängigen HALL-Konstanten \({R_{\rm{H}}}\).
Erklärung des Auftretens der Hall-Spannung
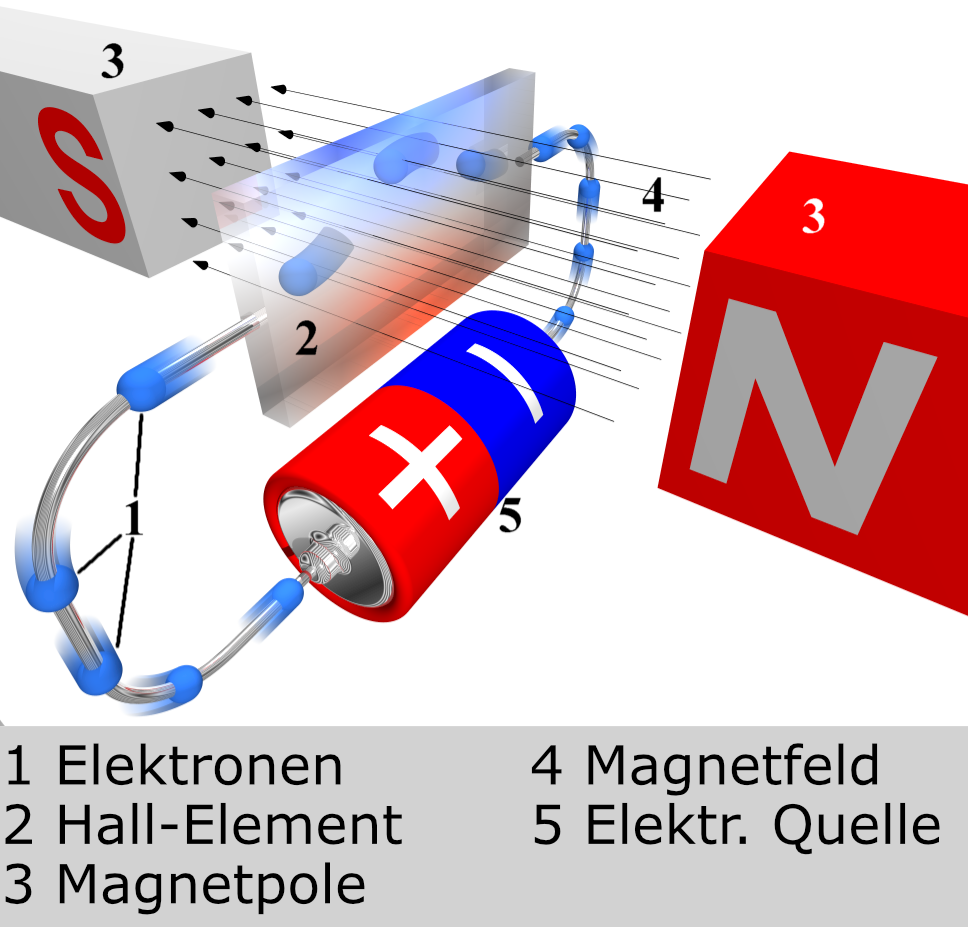
Fließt wie in Abb. 1 senkrecht zu einem Magnetfeld \(\vec{B}\) ein Strom \(I\), so wirkt auf die sich bewegenden Elektronen im Magnetfeld eine Lorentz-Kraft. Diese Kraft sorgt dafür, dass auf einer Seite des Hall-Elements ein Elektronenüberschuss (in Abb.1 oben blau markiert) entsteht, auf der anderen Seite ein Elektronenmangel (in Abb. 1 unten rot markiert). Dieser Ladungsunterschied (Potentialdifferenz) zwischen Ober- und Unterseite kann in Form einer Spannung zwischen Ober- und Unterseite gemessen werden.
Weiter sorgt der Ladungsunterschied zwischen Ober- und Unterseite des Hall-Elements aber auch für ein elektrisches Feld im Inneren des Hall-Elements. Auch das E-Feld übt eine Kraft auf die Elektronen aus. Allerdings wirkt diese Kraft gerade in die entgegengesetzte Richtung wie die Lorentz-Kraft. Wenn die Kraft auf die Elektronen durch das E-Feld betragsmäßig gleich der Lorentz-Kraft auf die sich bewegenden Elektronen im Magnetfeld ist, kommt es zu keiner weiteren Ladungstrennung. Es stellt sich ein fester Ladungsunterschied zwischen Ober- und Unterseite des Hall-Elements ein, die sog. Hall-Spannung \(U_{\rm{H}}\).
Ausgewählte HALL-Konstanten
In Tab. 1 findest du die HALL-Konstanten einiger Metalle.
| Metall | \(R_{\rm{H}}\) in \(10^{-11}\,\frac{\rm{m}^3}{\rm{C}}\) |
| Aluminium | \(-3{,}5\) |
| Bismut | \(-(5{,}3\,...\,6{,}8)\cdot 10^4\) |
| Blei | \(+0{,}9\) |
| Cadmium | \(+5{,}0\) |
| Gold | \(-7{,}2\) |
| Kupfer | \(-5{,}3\) |
| Palladium | \(-8{,}6\) |
| Platin | \(-2{,}0\) |
| Silber | \(-8{,}9\) |
| Wolfram | \(+11{,}8\) |
| Zink | \(+6{,}4\) |
| Zinn | \(-0{,}3\) |