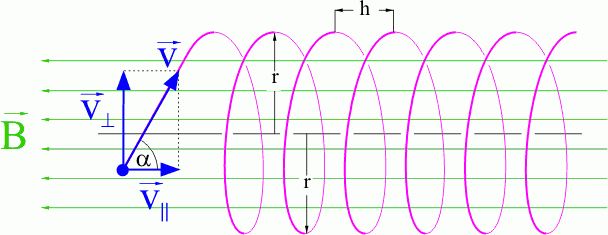
Schraubenlinie
Tritt ein geladenes Teilchen nicht senkrecht, also nicht unter einer Winkelweite von 90°, sondern schräg zu den Feldlinien in ein homogenes Magnetisches Feld ein, so durchläuft das Teilchen im B-Feld eine Schraubenlinie mit Radius \(r\) und Ganghöhe \(h\).
Berechnung des Radius \(r\) der Schraubenlinie
Der Betrag der zu \({\vec B}\) senkrechten Geschwindigkeitskomponente \({{{\vec v}_\bot }}\) ist \({v_\bot } = v \cdot \sin \left( \alpha \right)\). Beim Durchlaufen der Schraubenlinie trägt nur noch diese Geschwindigkeitskomponente zur LORENTZ-Kraft bei, die wiederum als Zentripetalkraft wirkt; somit gilt
\[{F_{\rm{L}}} = {F_{{\rm{ZP}}}} \Leftrightarrow q \cdot {v_ \bot } \cdot B = \frac{{m \cdot {v_ \bot }^2}}{r} \Leftrightarrow r = \frac{{m \cdot {v_ \bot }}}{{q \cdot B}} = \frac{{m \cdot v}}{{q \cdot B}} \cdot \sin \left( \alpha \right)\]
Berechnung der Umlaufdauer \(T\) für einen "Schraubengang"
Da die Umlaufdauer \(T\) unabhängig von der Geschwindigkeit \(v\) des Teilchens ist, ergibt sich hier der gleiche Ausdruck wie bei der Bewegung auf einer Kreisbahn:
\[T = \frac{{2 \cdot \pi \cdot m}}{{q \cdot B}}\]
Berechnung der Ganghöhe \(h\)
Der Betrag der zu \({\vec B}\) parallelen Geschwindigkeitskomponente \({{{\vec v}_\parallel }}\) ist \({v_\parallel } = v \cdot \cos \left( \alpha \right)\). Die Ganghöhe ist diejenige Strecke, welche das geladene Teilchen in der Zeit \(T\) mit dieser Geschwindigkeit vom Betrag \({v_\parallel }\) zurücklegt. Damit ergibt sich
\[h = {v_{||}} \cdot T = {v_{||}} \cdot \frac{{2 \cdot \pi \cdot m}}{{q \cdot B}} = \frac{{2 \cdot \pi \cdot m \cdot v}}{{q \cdot B}} \cdot \cos \left( \alpha \right)\]