Die Größenordnung der Avogadrozahl kannst du mit dem Ölfleckversuch bestimmen. Für eine präzisere Bestimmung eignet sich die Röntgenspektroskopie, da du mit der Drehkristallmethode von Bragg bei einem Einkristall den Netzebenenabstand \(d\) bestimmen kannst. Weißt du außerdem, wie der Einkristall aus den Atomen aufgebaut ist (Kristallstruktur) und kennst die Dichte der Substanz, aus welcher der Kristall aufgebaut ist, so kannst du die Avogadrozahl sehr genau bestimmen.
Kristall mit einfach kubischer Struktur
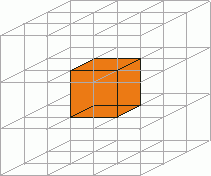
Einen Kristall mit einfach kubischer Struktur kannst du dir aus lauter gleich großen Würfeln aufgebaut denken, an dessen Eckpunkten Atome sitzen. Das gesamte Gitter eines Einkristalls ergibt sich aus einer kleinsten Einheit, der sog. Elementarzelle, wenn diese in allen Raumrichtungen immer wieder angesetzt wird (siehe Abb. 1). Auf diese Weise entsteht das gesamte Gitter des Einkristalls.
Polonium kristallisiert z.B. bei tiefen Temperaturen in einer einfach kubischen Struktur. In der Fachsprach wird diese Struktur oft mit sc für simple cubic kenntlich gemacht.
Bestimmung der AVOGADRO-Konstante
Für die Bestimmung der AVOGADRO-Konstante ist es nun wichtig zu wissen, wie viele Atome einer Elementarzelle zugeordnet werden müssen.
Die Animation in Abb. 2 zeigt dir, dass jedes Eckatom einer Zelle zu acht weiteren Zellen gehört. Dies bedeutet, dass ein Eckatom zu einem Achtel einer Zelle zuzuordnen ist.
In der würfelförmigen Elementarzelle gibt es acht Eckatome, also muss einer Elementarzelle genau ein Atom zugeordnet werden ( \(8 \cdot \frac{1}{8} = 1\) ).
Die Avogadrozahl erhält man nun durch die folgende Proportion:\[\frac{\text{Avogadrozahl}}{\text{Zahl der Teilchen in der Elementarzelle}} = \frac{\text{Volumen eines Kilomols}}{\text{Volumen der Elementarzelle}}\] \[\frac{{{N_A}}}{1} = \frac{{{V_{kmol}}}}{{{d^3}}} = \frac{{\frac{{{m_{kmol}}}}{\rho }}}{{{d^3}}} = \frac{{{m_{kmol}}}}{{\rho \cdot {d^3}}} = \frac{{{A_r}kg}}{{\rho \cdot {d^3}}}\]
Aufgabe
Erläutere, wieso bei einem einfachen kubischen Kristall jeder Elementarzelle genau ein Atom zugeordnet wird, obwohl eine Elementarzelle acht Eckatome besitzt.