THE HIGH FREQUENCY SPECTRA OF THE ELEMENTS
By H. G. J. Moseley, M. A.
Phil. Mag. (1913), p. 1024
In the absence of any available method of spectrum analysis, the characteristic types of X radiation, which an atom emits if suitably exited, have hitherto been described in terms of their absorption in aluminum. The interference phenomena exhibited by X-rays when scatted by a crystal have now, however, made possible the accurate determination of the frequencies of the various types of radiation. This was shown by W. H. and W. L. Bragg, who by this method analyzed the line spectrum emitted by the platinum target of an X-ray tube. C. G. Darwin and the author extended this analysis and also examined the continuous spectrum, which in this case constitutes the greater part of the radiation. Recently Prof. Bragg has also determined the wave-lengths of the strongest lines in the spectra of nickel, tungsten, and rhodium. The electrical methods which have hitherto been employed are, however, only successful where a constant source of radiation is available. The present paper contains a description of a method of photographing these spectra, which makes the analysis of the X-rays as simple as an other branch of spectroscopy. The author intends first to make a general survey of the principal types of high-frequency radiation, and then to examine the spectra of a few elements in greater detail and with greater accuracy. The results already obtained show that such data have an important bearing on the question of the internal structure of the atom, and strongly support the views of Rutherford and of Bohr.
Kaye has shown that an element excited by a stream of sufficiently fast cathode rays emits its characteristic X radiation. He used as targets a number of substances mounted on a truck inside an exhausted tube. A magnetic device enabled each target to be brought in turn into the line of fire. The apparatus was modified to suit the present work. The cathode stream was concentrated on to a small area of the target, and a platinum plate furnished with a fine vertical slit placed immediately in front of the part bombarded. The tube was exhausted by a Gaede mercury pump, charcoal in liquid air being also sometimes used to remove water vapor. The X-rays, after passing through the slit marked S in Fig. I, emerged through an aluminum window 0.02 mm. thick. The rest of the radiation was shut off by a lead box which surrounded the tube. The rays fell on the cleavage face, C, of a crystal of potassium ferrocyanide which was mounted on the prism-table of a spectrometer. The surface of the crystal was vertical and contained the geometrical axis of the spectrometer.
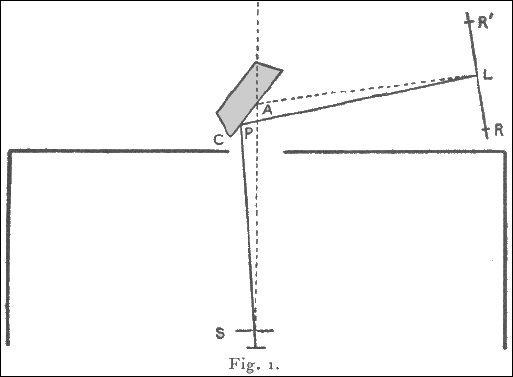
Now it is known that X-rays consist in general of two types, the heterogeneous radiation and characteristic radiations of definite frequency. The former of these is reflected from such a surface at all angles of incidence, but at the large angles used in the present work the reflexion is of very little intensity. The radiations of definite frequency, on the other hand, are reflected only when they strike the surface at definite angles, the glancing angle of incidence θ, the wave-length, and the "grating constant" d of the crystal being connected by the relation \[n \cdot \lambda = 2 \cdot d \cdot \sin\theta\]
where n, an integer, may be called the "order" in which the reflexion occurs. The particular crystal used, which was a fine specimen with face 6cm. square, was known to give strong reflexions in the first three orders, the third order being the most prominent.
If then a radiation of definite wave-length happens to strike any part P of the crystal at a suitable angle, a small part of it is reflected. Assuming for the moment that the source of the radiation is a point, the locus of P is obviously the arc of a circle, and the reflected rays will travel along the generating lines of a cone with apex at the image of the source. The effect on a photographic plate L will take the form of the arc of an hyperbola, curving away from the direction of the direct beam, With a fine slit at S, the arc becomes a fine line which is slightly curved in the direction indicated.
The photographic plate was mounted on the spectrometer arm, and both the plate and slit were 17cm. from the axis. The importance of this arrangement lies in a geometrical property, for when these two distances are equal the point L at which a beam reflected at a definite angle strikes the plate is independent of the position of P on the crystal surface. The angle at which the crystal is set is then immaterial so long as a ray can strike some part of the surface at the required angle. The angle θ can be obtained from the relation 2·θ = 180° - SPL = 180° - SAL.
The following method was used for measuring the angle SAL. Before taking a photograph a reference line R was made at both ends of the plate by replacing the crystal by a lead screen furnished with a fine slit which coincided with the axis of the spectrometer. A few seconds' exposure to the X-rays then gave a line R on the plate, and so defined on it the line joining S and A. A second line RQ was made in the same way after turning the spectrometer arm through a definite angle. The arm was then turned to the position required to catch the reflected beam and the angles LAP for any lines which were subsequently found on the plate. The angle LAR was measured with an error of not more than 0°. D, by superposing on the negative a plate on which reference lines had been marked in the same way at intervals of 1°. In finding from this the glancing angle of reflexion two small corrections were necessary in practice, since neither the face of the crystal nor the lead slit coincided accurately with the axis of the spectrometer. Wavelengths varying over a range of about 30 per cent. could be reflected for a given position of the crystal.
In almost all cases the time of exposure was five minutes. Ilford X-ray plates were used and were developed with rodinal. The plates were mounted in a plate-holder, the front of which was covered with black paper. In order to determine the wavelength from the reflexion angle θ it is necessary to know both the order n in which the reflexion occurs and the grating constant d. n was determined by photographing every spectrum both in the second order and the third. This also gave a useful check on the accuracy of the measurements; d cannot be calculated directly for the complicated crystal potassium ferrocyanide. The grating constant of this particular crystal had, however, previously been accurately compared with d', the constant of a specimen of rock-salt. It was found that \[d = 3 \cdot d' \cdot \frac{1988}{1985}\]
Now W.L. Bragg has shown that the atoms in a rock-salt crystal are in simple cubical array. Hence the number of atoms per c.c. \[2\cdot \frac{N \cdot \sigma}{M} = \frac{I}{(d')^3}\]
N, the number of molecules in a gram-mol., = 6.05·1023 assuming the charge on an electron to be 4.89 x 10¯10; σ, the density of this crystal of rock-salt, was 2.167, and M the molecular weight = 58.46.
This gives d' = 2.814 x 10¯8 and d = 8.454 x 10¯8 cm. It is seen that the determination of wave-length depends on so that the effect of uncertainty in the value of this quantity will not be serious. Lack of homogeneity in the crystal is a more likely source of error, as minute inclusions of water would make the density greater than that found experimentally.
Twelve elements have so far been examined....
Plate V shows the spectra in the third order placed approximately in register. Those parts of the photographs which represent the same angle of reflexion are in the same vertical line.... It is to be seen that the spectrum of each element consists of two lines. Of these the stronger has been called α in the table, and the weaker ß. The lines found on any of the plates besides α and ß were almost certainly all due to impurities. Thus in both the second and third order the cobalt spectrum shows Niα very strongly and Fe faintly. In the third order the nickel spectrum shows Mnα faintly. The brass spectra naturally show α and ß both of Cu and of Zn, but Znß2 has not yet been found. In the second order the ferro-vanadium and ferro-titanium spectra show very intense third-order Fe lines, and the former also shows Cuα3 faintly. The Co contained Ni and 0.8 per cent. Fe, the Ni 2.2 per cent. Mn, and the V only a trace of Cu. No other lines have been found, but a search over a wide range of wave-lengths has been made only for one or two elements, and perhaps prolonged exposures, which have not yet been attempted, will show more complex spectra. The prevalence of lines due to impurities suggests that this may prove a powerful method of chemical analysis. Its advantage over ordinary spectroscopic method lies in the simplicity of the spectra and the impossibility of one substance masking the radiation from another. It may even lead to the discovery of missing elements, as it will be possible to predict the position of their characteristic lines.....
Phil. Mag. (1914), p. 703.
The first part of this paper dealt with a method of photographing X-ray spectra, and included the spectra of a dozen elements. More that thirty other elements have now been investigated, and simple laws have been found which govern the results, and make it possible to predict with confidence the position of the principal lines in the spectrum of any element from aluminum to gold. The present contribution is a general preliminary survey, which claims neither to be complete nor very accurate....
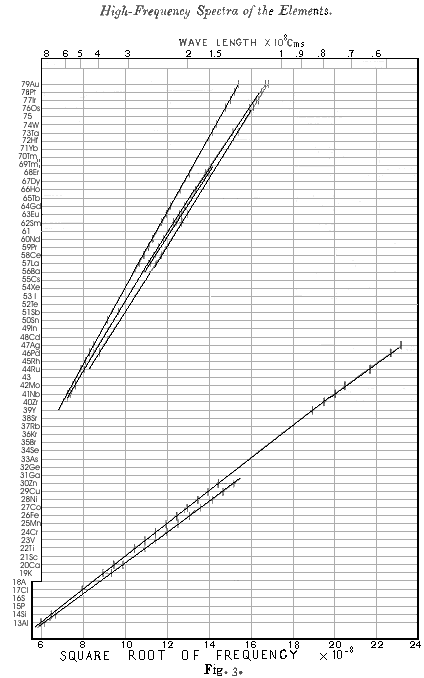
The results obtained for radiations belonging to Barkla's K series are given in table I, and for convenience the figures already given in Part I. are included. The wave-length λ has been calculated from the glancing angle of reflexion θ by means of the relation \(n\cdot \lambda = 2\cdot d \cdot \sin\theta\), where d has been taken to be 8.454 x 10¯8 cm. As before, the strongest line is called α and the next line ß. The square root of the frequency of each line is plotted in Fig. 3, and the wavelengths can be read off with the help of the scale at the top of the diagram.
|
Table I
|
||||
|
α line
λx108 cm |
QK
|
N Atomic
Number |
ß line
λ x 108 cm |
|
| Aluminum |
8.364
|
12.05
|
13
|
7.912
|
| Silicon |
7.142
|
13.04
|
14
|
6.729
|
| Chlorine |
4.750
|
16.00
|
17
|
-------
|
| Potassium |
3.759
|
17.98
|
19
|
3.463
|
| Calcium |
3.368
|
19.00
|
20
|
3.094
|
| Titanium |
2.758
|
20.99
|
22
|
2.524
|
| Vanadium |
2.519
|
21.96
|
23
|
2.297
|
| Chromium |
2.301
|
22.98
|
24
|
2.093
|
| Manganese |
2.111
|
23.99
|
25
|
1.818
|
| Iron |
1.946
|
24.99
|
26
|
1.765
|
| Cobalt |
1.798
|
26.00
|
27
|
1.629
|
| Nickel |
1.662
|
27.04
|
28
|
1.506
|
| Copper |
1.549
|
28.01
|
29
|
1.402
|
| Zinc |
1.445
|
29.01
|
30
|
1.306
|
| Yttrium |
0.838
|
38.1
|
39
|
-------
|
| Zirconium |
0.794
|
39.1
|
40
|
-------
|
| Niobium |
0.750
|
40.2
|
41
|
-------
|
| Molybdenum |
0.721
|
41.2
|
42
|
-------
|
| Ruthenium |
0.638
|
43.6
|
44
|
-------
|
| Palladium |
0.584
|
45.6
|
46
|
-------
|
| Silver |
0.560
|
46.6
|
47
|
-------
|
The spectrum of Al was photographed in the first order only. The very light elements give several other fainter lines, which have not yet been fully investigated, while the results for Mg and Na are quite complicated, and apparently depart from the simple relations which connect the spectra of the other elements.
|
Table II
|
||||||
|
α line
λ x 108 cm |
QL
|
N Atomic
Number |
ß line
λ x 108 cm |
Φ line
λ x 108 cm |
γ line
λ x 108 cm |
|
| Zirconium |
6.091
|
32.8
|
40
|
---
|
---
|
---
|
| Niobium |
5.749
|
33.8
|
41
|
5.507
|
---
|
---
|
| Molybdenum |
5.423
|
34.8
|
42
|
5.187
|
---
|
---
|
| Ruthenium |
4.861
|
36.7
|
44
|
4.660
|
---
|
---
|
| Rhodium |
4.622
|
37.7
|
45
|
---
|
---
|
---
|
| Palladium |
4.385
|
38.7
|
46
|
4.168
|
---
|
3.928
|
| Silver |
4.170
|
39.6
|
47
|
---
|
---
|
---
|
| Tin |
3.619
|
42.6
|
50
|
---
|
---
|
---
|
| Antimony |
3.458
|
43.6
|
51
|
3.245
|
---
|
---
|
| Lanthanum |
2.676
|
49.5
|
57
|
2.471
|
2.424
|
2.313
|
| Cerium |
2.567
|
50.6
|
58
|
2.366
|
2.315
|
2.209
|
| Praseodymium |
(2.471)
|
51.5
|
59
|
2.265
|
---
|
---
|
| Neodymium |
2.382
|
52.5
|
60
|
2.175
|
---
|
---
|
| Samarium |
2.208
|
54.5
|
62
|
2.008
|
1.972
|
1.893
|
| Europium |
2.130
|
55.5
|
63
|
1.925
|
1.888
|
1.814
|
| Gadolinium |
2.057
|
65.5
|
64
|
1.853
|
1.818
|
---
|
| Holmium |
1.914
|
58.6
|
66
|
1.711
|
---
|
---
|
| Erbium |
1.790
|
60.6
|
68
|
1.591
|
1.563
|
---
|
| Tantalum |
1.525
|
65.6
|
73
|
1.330
|
---
|
1.287
|
| Tungsten |
1.486
|
66.5
|
74
|
---
|
---
|
---
|
| Osmium |
1.397
|
68.5
|
76
|
1.201
|
---
|
1.172
|
| Iridium |
1.354
|
69.6
|
77
|
1.155
|
---
|
1.138
|
| Platinum |
1.316
|
70.6
|
78
|
1.121
|
---
|
1.104
|
| Gold |
1.287
|
71.4
|
79
|
1.092
|
---
|
1.078
|
In the spectra from yttrium onwards only the α line has so far been measured, and further results in these directions will be given in a later paper. The spectra both of K and of Cl were obtained by means of a target of KCl, but it is very improbable that the observed lines have been attributed to the wrong elements. The α line for elements from Y onwards appeared to consist of a very close doublet, an effect previously observed by Bragg in the case of Rhodium.
The results obtained for the spectra of the L series are given in Table II and plotted in Fig. 3. These spectra contain five lines, α, ß, γ, δ, ε, reckoned in order of decreasing wave-length and deceasing intensity. There is also always a faint companion α' on the long wave-length side of α, a rather faint line Φ between ß and γ for the rare earth elements at least, and a number of very faint lines of wave-length greater than α. Of these, α, ß, Φ, and γ have been systematically measured with the object of finding out how the specturm alters from one element to another. The fact that often values are not given for all these lines merely indicates the incompleteness of the work. The spectra, so far as they have been examined, are so entirely similar that without doubt α, ß, and γ at least always exist. Often γ was not included in the limited range of wave-lengths which can be photographed on one plate. Sometimes lines have not been measured, either on account of faintness or of the confusing proximity of lines due to impurities....
Conclusions
In Fig. 3 the spectra of the elements are arranged on horizontal lines spaced at equal distances. The order chosen for the elements is the order of the atomic weights, except in the cases of A, Co, and Te, where this clashes with the order of the chemical properties. Vacant lines have been left for an element between Mo and Ru, an element between Nd and Sa, and an element between W and Os, none of which are yet known, while Tm, which Welsbach has separated into two constituents, is given two lines. This equivalent to assigning to successive elements a series of successive characteristic integers. On this principle the integer N for Al, the thirteenth element, has been taken to be 13, and the values of N then assumed by the other elements are given on the left-hand side of Fig. 3 This proceeding is justified by the fact that it introduces perfect regularity into the X-rays spectra. Examination of Fig 3. shows that the values of ν1/2 for all the lines examined both in the K and the L series now fall on regular curves which approximate to straight lines. The same thing is shown more clearly by comparing the values of N in Table I with those of \[Q_K = \sqrt{\frac{v}{\frac{3}{4} v_0}}\]
ν being the frequency of the line and νo the fundamental Rydberg frequency. It is here plain that QK = N - 1 very approximately, except for the radiations of very short wave-length which gradually diverge from this relation. Again, in Table II a comparison of N with \[Q_L = \sqrt{\frac{v}{\frac{5}{36} v_0}}\]
where ν is the frequency of the Lα line, shows that QL = N - 7.4 approximately, although a systematic deviation clearly shows that the relation is not accurately linear in this case.
Now if either the elements were not characterized by these integers, or any mistake had been made in the order chosen or in the number of places left for unknown elements, these regularities would at once disappear;. We can therefore conclude from the evidence of the X-ray spectra alone, without using any theory of atomic structure, that these integers are really characteristic of the elements. Further, as it is improbable that two different stable elements should have the same integer, three, and only three, more elements are likely to exist between Al and Au. As the X-ray spectra of these elements can be confidently predicted, they should not be difficult to find. The examination of keltium would be of exceptional interest, as no place has been assigned to this element.
Now Rutherford has proved that the most important constituent of an atom is its central positively charge nucleus, and van den Broek has put forward the view that the charge carried by this nucleus is in all cases an integral multiple of the charge on the hydrogen nucleus. There is every reason to suppose that the integer which controls the X-ray spectrum is the same as the number of electrical units in the nucleus, and these experiments therefore give the strongest possible support to the hypothesis of van den Broek. Soddy has pointed out that the chemical properties of the radio-elements are strong evidence that this hypothesis is true for the elements from thallium to uranium, so that its general validity would now seem to be established.

