Quantenmechanischen Betrachtung des Wasserstoffatoms
Beim Wasserstoffatom hält sich ein einzelnes Elektron im Coulomb-Potential des Atomkerns auf. Es kann dabei nicht beliebige Energiewerte annehmen - seine Energie ist quantisiert.
Die exakte quantenmechanische Berechnung der erlaubten Energiewerte mit Hilfe der Schrödingergleichung kann mit der in der Schule gelernten Mathematik nicht durchgeführt werden. Auf der Seite des milq-Projektes ist die exakte Berechnung erläutert.
In einem ersten Schritt lassen wir uns daher einfach die Schrödingergleichung von einem Programm für vorgegebene Energiewerte ausrechnen. Die Lösung interpretieren wir unter folgendem Gesichtspunkt: Da das Quadrat der Psi-Funktion \(|{\Psi (r)|}^2\) ein Maß für die Aufenthaltswahrscheinlichkeit darstellt, ist es eine zwingende Randbedingung, dass die Aufenthaltswahrscheinlichkeit im Unendlichen Null ist. Damit muss auch \(\Psi(\infty)=0\) sein.
Wir müssen die Energiewerte daher so lange variieren, bis die Psi-Funktion \(\Psi(r)\) im Unendlichen Null wird. Nur solche Energiewerte sind physikalisch sinnvolle Lösungen der Schrödinger-Gleichung. Man nennt sie Eigenwerte der Differentialgleichung.
Programm: Schrödingers Schlange
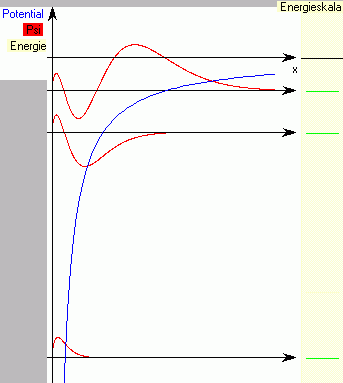
Die Windows-Software Schrödingers Schlange von Dr. J. Küblbeck löst die Schrödingergleichung für ein Elektron. Mit Hilfe von Reglern kannst du die Energie des Elektrons so fein einstellen, dass die \(\Psi\)-Funktion beschränkt bleibt. Dies liefert die Energiewerte. In Abb. 1 siehst du die Endergebnisse des Programms für \(n=1\), \(n=2\) und \(n=3\) übereinander kopiert.
Aufgabe
Bestimme mit dem Programm die Energieeigenwerte für \(n=1\), \(n=2\), \(n=3\) und \(n=4\) und vergleiche sie mit den Werten nach Bohr, die sich aus \(E_n=\frac{-13{,}6\,\rm{eV}}{n^2}\) ergeben.
Programm Schrödingergleichung von Matthias Borchardt
Das modernere Programm zur Schrödingergleichung von Matthias Borchardt funktioniert auf sehr ähnliche Art und Weise. Auch hier können die Eigenwerte der Schrödingergleichung fürs Wasserstoffatom mit den Drehimpulsen \(\ell=0,1,2,3,4\) durch Einstellen der Energie ermittelt werden. Zusätzlich kann das Programm auch bei den Lösungen die radiale Aufenthaltswahrscheinlichkeit als Orbitale veranschaulichen.
Das für Windows verfügbare Programm kann hier heruntergeladen werden.