Nach der Schrödingergleichung gibt es verschiedene stationäre Zustände des Atoms, die sich durch vier verschiedene Quantenzahlen ausdrücken lassen:
| Bezeichnung | Bedingung | Bemerkung | |
| n | Hauptquantenzahl | \[n \in \mathbb{N}\] | Die Hauptquantenzahl n bestimmt im wesentlichen die Energie En des beschriebenen Zustands |
| l | Nebenquantenzahl | l = 0; 1; 2; . . . (n-1) | Die Nebenquantenzahl beschreibt den Betrag des Bahndrehimpulses. Oft werden für die Nebenquantenzahl auch Buchstaben verwendet: l = 0: s ; l = 1: p ; l = 2: d und l = 3: f. |
| m | Magnetische Quantenzahl | -l ≤ m ≤ +l | Quantenzahl für die z-Komponente des Drehimpulses |
| s | Spin-Quantenzahl | s = +½; s = -½ | Quantenzahl für den Eigendrehimpuls eines Elektrons |
Entwickle eine übersichtliche Tabelle, mit der die Zahl der möglichen Elektronenzustände für die Hauptquantenzahlen n =1, n = 2 und n = 3 unter Berücksichtigung der oben aufgeführten Bedingungen ermittelt werden kann.
Jeder Quantenzahlkombination lässt sich demnach eine Aufenthaltswahrscheinlichkeit zuordnen. Solche Aufenthaltswahrscheinlichkeiten kann man auf verschiedene Weise darstellen.
Darstellung als radiale Funktion
|
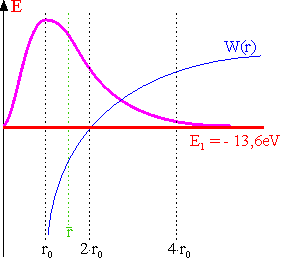
Grundzustand: n = 1;
|
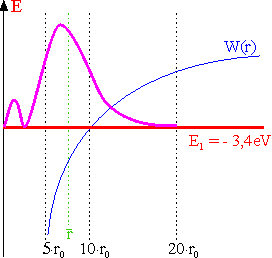
1. Anregungszustand: n = 2;
|
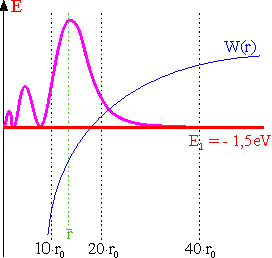
2. Anregungszustand: n = 3;
|
|
l = 0
|
z.B.: l = 0
|
z.B.: l = 0
|
|
Radiale Aufenthaltswahrscheinlichkeit im 1s-Zustand
|
Radiale Aufenthaltswahrscheinlichkeit im 2s-Zustand
|
Radiale Aufenthaltswahrscheinlichkeit im 3s-Zustand
|
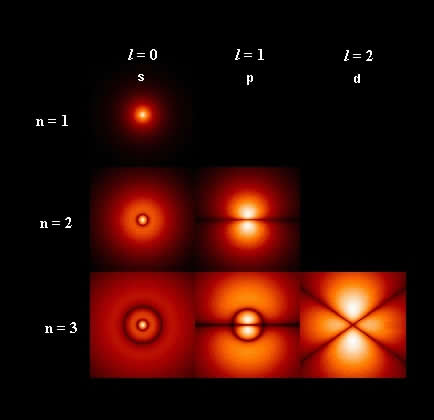
Flächig dargestellte Wahrscheinlichkeitsverteilung
|
Die rechte Darstellung zeigt, dass es für die verschiedenen Quantenzahlen sehr unterschiedliche Wahrscheinlichkeitsverteilungen gibt:
|
 |
Räumliche Darstellung
Die folgenden Abbildungen stammen von Gerhard März vom Friedrich König Gymnasium, Würzburg.
 n = 1; l = 0; m = 0 |
|
|
|
|
|
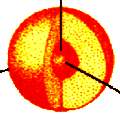 n = 2; l = 0; m = 0 |
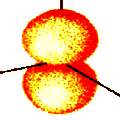 n = 2; l = 1; m = 0 |
 n = 2; l = 1; m = 1 |
|
|
|
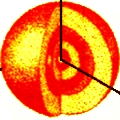 n = 3; l = 0; m = 0 |
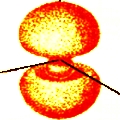 n = 3; l = 1; m = 0 |
 n = 3; l = 1; m = 1 |
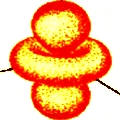 n = 3; l = 2; m = 0 |
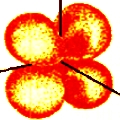 n = 3; l = 2; m = 1 |
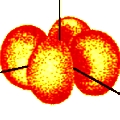 n = 3; l = 2; m = 2 |
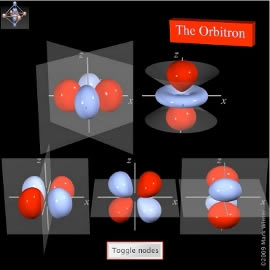
Auswahl einiger gut aufbereiteter Seiten zu den Orbitalen im Internet
|
|
|
|
|
 |
|
 |