Quantenmech. Atommodell

Großteils nach dem milq-Projekt - nur für besonders Interessierte

Im Folgenden wird ein Weg nachvollzogen, wie er durch das milq-Projekt vorgeschlagen wurde. Er wurde auf die wesentlichen Inhalte der H-Atom-Berechnung des milq-Projekts reduziert und um die endgültige Energieberechnung ergänzt.

Potentialtopf statt Coulomb-Potential: Zunächst ersetzen wir das klassische Coulomb-Potential durch einen geschickt gewählten, diesem ähnlichen Potentialtopf mit unendlich hohen Potentialwänden. Genauer gesagt handelt es sich um einen dreidimensionalen, kugelförmigen Potentialtopf (die Topfwände sind die vierte Dimension) mit Radius R. Innerhalb der Kugel besitzt das Potential einen konstanten Wert, außerhalb ist es unendlich. Dieses Modellpotential besitzt den Kugelradius R und die Energiedifferenz W0 zwischen dem "Boden" des Potentialtopfs und dem Energienullpunkt als freie Parameter. Diese beiden Parameter werden so variiert, dass das Coulomb-Potential möglichst gut genähert wird.

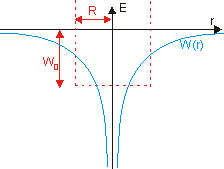eindimensionaler Vergleich

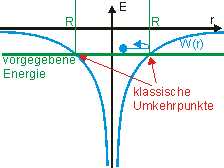
Radiusanpassung des Potentialtopfs: Klassisch kann sich ein Elektron nur soweit vom Kern entfernen, bis es keine kinetische Energie mehr hat, seine Gesamtenergie also nur mehr potentielle ist. In diesem "Umkehrpunkt" gilt: \(E =  - \frac{{{e^2}}}{{4\pi {\varepsilon _0} \cdot R}} \Rightarrow R =  - \frac{{{e^2}}}{{4\pi {\varepsilon _0} \cdot E}}\). Ein klassisches Teilchen kann in den Bereich r > R nicht eindringen, denn dort wäre seine potentielle Energie größer als seine Gesamtenergie. Rmax hängt also von der Energie E ab. In unserem Modell wird das Coulomb-Potential durch einen Potentialtopf mit dem Durchmesser 2·R ersetzt. Das bedeutet: Innerhalb dieses Bereichs wird das Potential als konstant angenommen; der Außenbereich ist für das Elektron unzugänglich (unendlich hohe Potentialwände).

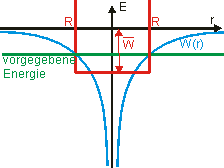
Ermitteln der Tiefe W0 des Potentialtopfs: Innerhalb des Potentialtopfs hat das Potential einen konstanten Wert W0. Der Potentialtopf nähert das Coulomb-Potential am besten an, wenn man W0 so wählt, dass es die "mittlere Tiefe" des Coulomb-Potentials darstellt. Dazu berechnet man den Mittelwert \({\bar W}\) des Coulomb-Potentials über eine Kugel mit Radius R: \[\bar W = \frac{1}{V} \cdot \int {W(\vec x){d^3}x} \] Das Ergebnis der Integration ist: \[\bar W =  - \frac{3}{2} \cdot \frac{{{e^2}}}{{4\pi {\varepsilon _0} \cdot R}} = \frac{3}{2}E = {W_0}\] . Wen die Integration interessiert, findet dies auf der milq-Seite. Man kann das Grundprinzip der Herleitung aber auch verstehen, wenn man nur anerkennt, dass W0 = const. · E ist.

Berechnung der Energieniveaus
Wir berechnen statt des Kugelpotentialtopfs einen Würfelpotentialtopf mit Kantenlänge \(2\cdot R\). Dies führt zu Veränderungen bei den geometriebedingten Konstanten, nicht aber bei den physikalischen Konstanten.
Die Energieniveaus beim dreidimensionalen "Würfel"-Potentialtopf sind (siehe Seite dreidimensionaler Potentialtopf):
\[E = \frac{{{h^2}}}{{8 \cdot m \cdot {{\left( {2R} \right)}^2}}} \cdot \left( {{n_x}^2 + {n_y}^2 + {n_z}^2} \right) + {W_0}\]
Dabei ist m die Elektronenmasse und n_x, n_y, n_z sind ganze Zahlen, die den Zustand des Elektrons im Potentialtopf kennzeichnen (Quantenzahlen). Wir beschränken uns auf Zustände, die keine Raumrichtung auszeichnen. Dann gilt n_x = n_y = n_z = n, so dass der Elektronenzustand durch eine einzige Quantenzahl n beschrieben wird.
Die Energieniveaus werden dann
\[E = \frac{{{h^2}}}{{8 \cdot m \cdot {{\left( {2R} \right)}^2}}} \cdot 3{n^2} + {W_0}\]
Ersetzen wir in dieser Gleichung W₀ durch c·E (hier) mit c = 1,5 und \(R =  - \frac{{{e^2}}}{{4\pi {\varepsilon _0} \cdot E}}\), wodurch man im Prinzip einen Potentialtopf erhält, dessen R sich für die einzelnen Quantenzustände dem entsprechenden Coulomb-Potential anpasst, so folgt:
\[E = \frac{{{h^2} \cdot 3{n^2}}}{{8 \cdot m \cdot {{\left( {2R} \right)}^2}}} + {W_0} = \frac{{{h^2} \cdot 3{n^2}}}{{8 \cdot m \cdot 4 \cdot {R^2}}} + \frac{3}{2}E \Rightarrow \]
\[\frac{1}{2}E =  - \frac{{{h^2} \cdot 3{n^2}}}{{32 \cdot m \cdot {R^2}}} \Rightarrow E =  - \frac{{{h^2} \cdot 3{n^2}}}{{16 \cdot m \cdot {R^2}}}\]
Mit \(R =  - \frac{{{e^2}}}{{4\pi {\varepsilon _0} \cdot E}}\) folgt dann
\[E = \frac{{{h^2} \cdot 3{n^2} \cdot 16 \cdot {\pi ^2} \cdot {\varepsilon _0}^2 \cdot {E^2}}}{{16 \cdot m \cdot {e^4}}}\]
und daraus
\[E = \frac{{m \cdot {e^4}}}{{{h^2} \cdot 3{n^2} \cdot {\pi ^2} \cdot {\varepsilon _0}^2}} = \frac{{m \cdot {e^4}}}{{{h^2} \cdot 3 \cdot {\pi ^2} \cdot {\varepsilon _0}^2}} \cdot \frac{1}{{{n^2}}}\]
Man erkennt dabei die korrekte Abhängigkeit der Energie von E ~ 1/n², sowie die korrekte Abhängigkeit von den Naturkonstanten m, e², h und ε₀².
Dass hier die Konstanten nicht mit den "wahren" Konstanten übereinstimmen, liegt an der Verwendung der verschiedenen Näherungen wie "Potentialtopf statt Coulomb-Potential" und "Würfel-Potential statt des Kugel-Potential".
Kritisch anzumerken ist, dass man die Energie, die man als Ergebnis haben will, vorher hineinsteckt und dass der zunächst angenommene einzige Potentialtopf eigentlich für jeden Energieeigenwert seinen Radius und seine Tiefe ändert, sodass man eigentlich einen stufenförmigen Potentialtopf besitzt.