|
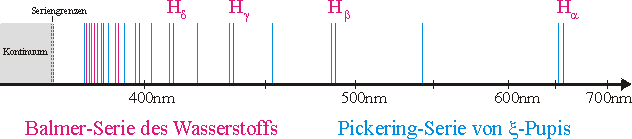
Im Jahre 1897 stellte der amerikanische Astronom Pickering im Licht des Sterns ξ-Puppis eine Spektralserie fest (in der Abbildung "blau" dargestellt), die viel mit der Balmer-Serie des Wasserstoffs (in der Abbildung "lila" dargestellt) gemeinsam hat.
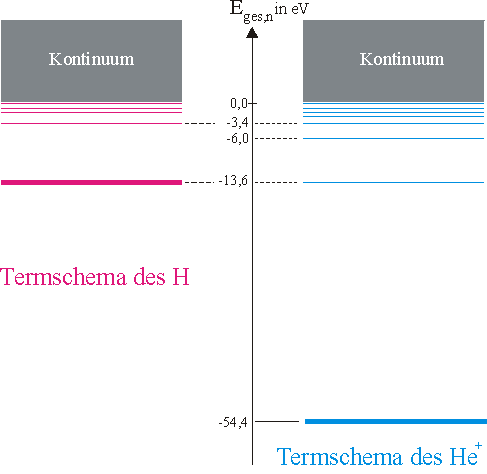
Man sieht: Jede zweite Linie der Pickering-Serie fällt mit einer Linie der Balmer-Serie fast zusammen Zwischen zwei Balmer-Linien befindet sich stets eine zusätzliche Linie der Pickering-Serie Rydberg konnte zeigen, dass für die Linien der Pickering-Serie ein ähnliches Gesetz gilt wie für die Balmer-Serie des Wasserstoffs. Jedoch nimmt die Laufvariable k in diesem Gesetz nicht nur positive ganzzahlige sondern auch halbzahlige Werte an: Für die Gesamtenergie eines Elektrons auf der \(n\)-ten Quantenbahn eines Einelektronensystems mit der Kernladung \(Z \cdot \)e gilt Beim Übergang von der \(m\)-ten zur \(n\)-ten Quantenbahn (\(m > n\)) wird ein Photon der Energie \(h \cdot f\) emittiert. Dabei gilt In der folgenden Abbildung sind die beiden Termschemata für Wasserstoff und einfach ionisiertes Helium gegenübergestellt:
Die oben entwickelten Gedanken lassen sich auch auf Einelektronensysteme wie Li++ und Be+++ anwenden. Allerdings wird durch diese Theorie noch nicht erklärt, warum jede zweite Linie des Wasserstoff- und He+-Spektrums nicht exakt zusammenfallen. Lesen Sie hierzu die Seite über die Kernmitbewegung. |
Der geringfügige Unterschied zwischen den BALMER-Linien des Wasserstoffs und den entsprechenden Linien der PICKERING-Serie erklärt sich aus den unterschiedlichen Massen des Wasserstoffkerns und des Heliumkerns.
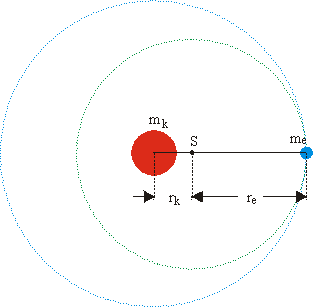
In der einfachen Herleitung des Atommodells von BOHR wurde davon ausgegangen, dass das Elektron um den Kernmittelpunkt kreist. Dies wäre jedoch nur bei sehr schweren (im Grenzfall "unendlich" schweren) Kernen richtig. Tatsächlich müssten in diesem Modell Kern und Elektron um den gemeinsamen Schwerpunkt S kreisen.
|
Um die bisher entwickelte Theorie weiter benutzen zu können (Elektron kreist um den Kernmittelpunkt) wird die Elektronenmasse \({m_e}\) durch die sogenannte reduzierte Masse \(m'\) ersetzt. Bei der Bestimmung von \(m'\) geht man davon aus, dass \(m'\) bei der Rotation um den Kernmittelpunkt (Radius \({r_e} + {r_{\rm{K}}}\)) die gleiche Zentripetalkraft erfahren muss, wie das Elektron der Masse \({m_e}\) bei der Rotation um den gemeinsamen Schwerpunkt S: Für die Berechnung der Spektralserien hast du beim Einelektronensystem die Beziehung
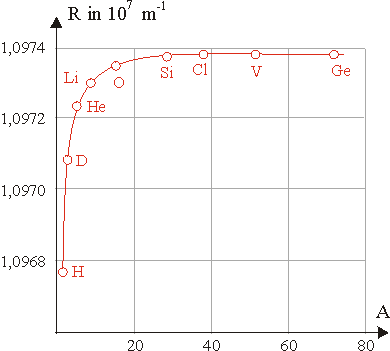
Die nebenstehende Abbildung zeigt den Verlauf der Rydbergkonstanten in Abhängigkeit von der Ordnungszahl (bzw. Massezahl) \(A\). Hinweis: Mit einem hochauflösenden Spektrographen entdeckte man bei den Linien des Wasserstoffspektrums noch sogenannte Satellitenlinien. Sie sind auf das im natürlichen Isotopengemisch vorhandene Deuterium (schwerer Wasserstoff) zurückzuführen. |