Sicher hast du schon einmal auf einer Pfütze einen dünnen Ölfilm beobachtet, der - bei schräger Draufsicht - in allen Farben schimmert. Der Grund für die manchmal sehr eindrucksvolle Farberscheinung wird dir erst in der Oberstufe näher erläutert. Voraussetzung für die Entstehung des Farbeindrucks ist es, dass der Ölfilm auf dem Wasser sehr dünn ist. Wie dir im Folgenden gezeigt wird, kann man über die Ausbildung extrem dünner Ölschichten auf dem Wasser die Größenordnung des Atomdurchmessers abschätzen.
Modellexperiment mit Backerbsen
Hinweis: Das Modellexperiment funktioniert natürlich auch mit getrockneten Erbsen oder ähnlichen kleinen, runden Gegenständen.
Um das Grundprinzip des Versuchs besser zu verstehen, betrachten wir zunächst keine nicht sichtbaren Atome oder Moleküle, sondern Backerbsen. Wir wollen versuchen, den durchschnittlichen Durchmesser der Backerbsen mithilfe eines Experimentes zu bestimmen.
Aufbau, Durchführung und Beobachtung
Zuerst schütten wir wie in Abb. 2/1 gerade so viele Backerbsen in eine Schale mit bekannter Grundfläche \(A\), dass sich eine einlagige Schicht aus Backerbsen bildet.
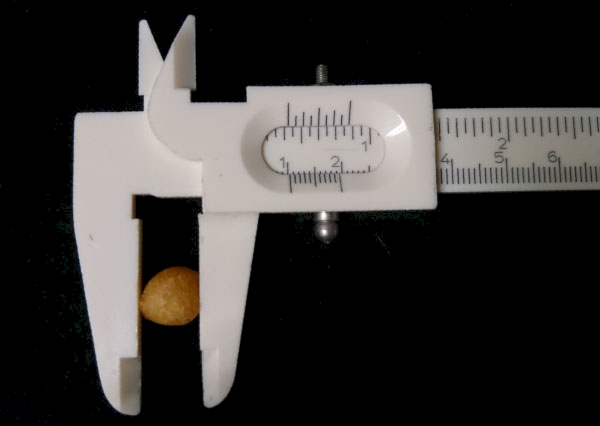
Anschließend füllen wir die Backerbsen aus der Schale in einen Messzylinder und ermittelt so das Volumen \(V\) der Erbsen (Abb. 2/2).
Mit \(V = A \cdot h \Leftrightarrow h = \frac{V}{A}\) können wir nun die Höhe der Backerbsenschicht in der Schale und - da die Schicht nur aus einer Lage Backerbsen bestand - den durchschnittlichen Durchmesser der Backerbsen rechnerisch bestimmen.
Auswertung
In unserem Fall gilt daher für den durchschnittliche Backerbsendurchmesser \(h\)\[h = \frac{V}{A}\Rightarrow h=\frac{250\,\rm{cm}^3}{18\,\rm{cm}\cdot 14\,\rm{cm}}\approx 1\,\rm{cm}\]
Am Modell der Backerbsen können wir nun unser Ergebnis auch mit einer direkten Messung prüfen. Dieser Schritt ist bei Atomen natürlich nicht möglich.
Ölfleckversuch
Aufbau und Durchführung
Beim Ölfleckversuch geht man analog, lediglich in einer anderen Reihenfolge vor:
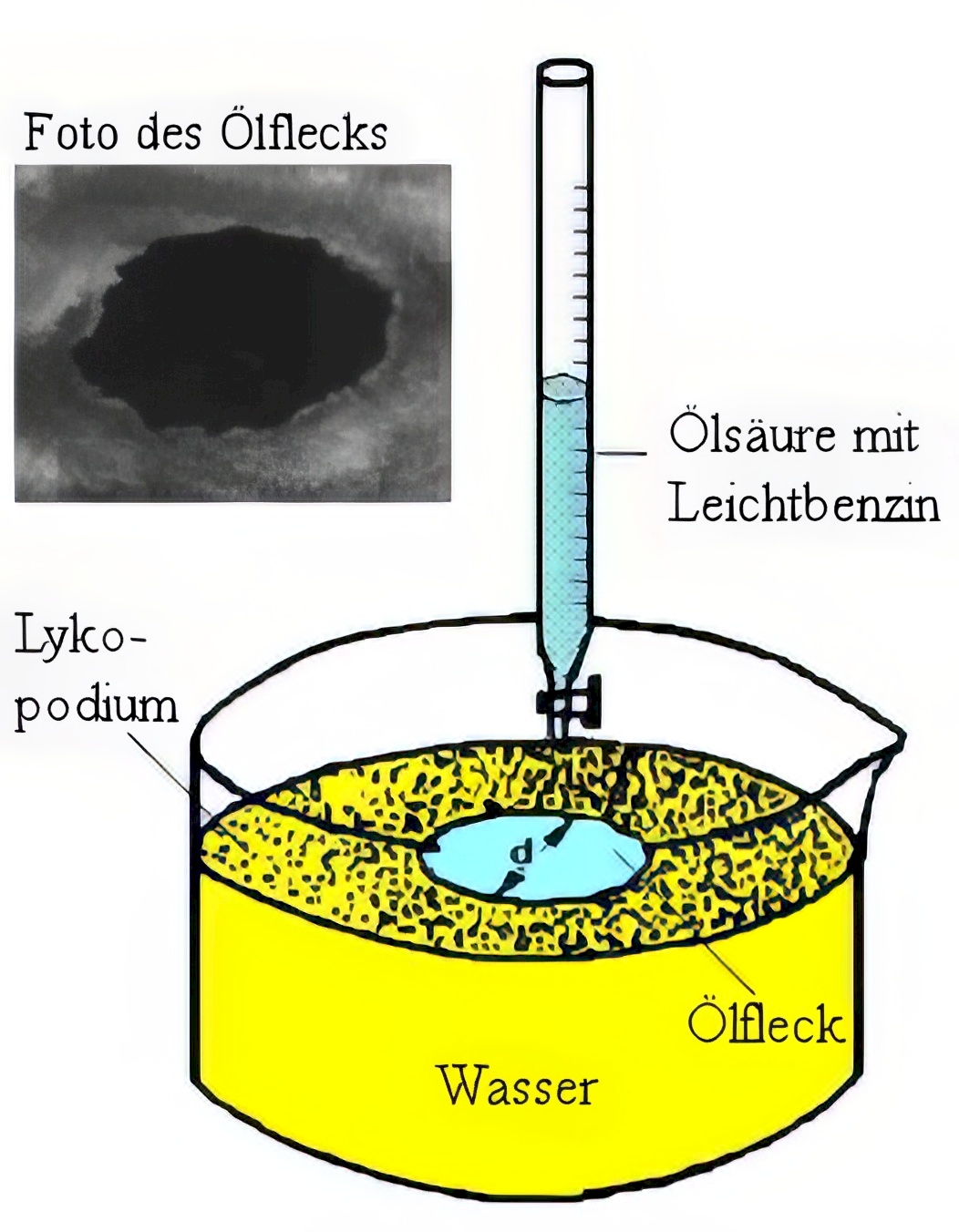
Zuerst lässt man einen Tropfen eines Ölsäure-Leichtbenzin-Gemisches mit bekanntem Volumen \(V\) mittels einer Tropfbürette auf eine ruhige ebene Wasseroberfläche auftropfen, die vorher mit Lykopodium (Bärlappsporen) bestreut war. Der Tropfen der Mischung breitet sich kreisförmig aus, der dünne Film ist aber aus mikroskopischer Sicht ein Zylinder.
Nach dem Verdampfen des Leichtbenzins verringert sich der Kreisdurchmesser auf den Wert \(d\), aus dem man leicht mittels \(A = \pi \cdot {\left( {\frac{d}{2}} \right)^2}\) den Flächeninhalt \(A\) bestimmen kann. Wenn man nun davon ausgeht, dass sich auf dem Wasser eine einmolekulare Schicht von Ölsäuremolekülen ausgebildet hat, kann man - ähnlich wie bei den Erbsen - den Durchmesser eines Moleküls durch \(h = \frac{V}{A}\) abschätzen.
Beobachtung
Die Animation in Abb. 6 zeigt den Aufbau, die Durchführung und die Beobachtungen des Ölfleckversuchs. Aus ihr kannst du die Werte für die spätere Auswertung des Experiments entnehmen.
Auswertung
Aufgabe
Beobachte die Anzahl \(N\) der Tropfen des Ölsäure-Leichtbenzins, die in der Animation in Abb. 5 in das kleine Schälchen tropfen, und deren Volumen \(V_{\rm{N}}\).
Berechne mit diesen Werten das Volumen \(V\) eines Tropfens.
Berechne das Volumen \(V_{\rm{Ölsäure}}\) des nach der Verdunstung des Leichtbenzins zurückbleibenden Ölsäureflecks, wenn das Ölsäure-Leichtbenzin-Gemisch ein Volumenverhältnis \(\frac{{{V_{{\rm{Ölsäure}}}}}}{{{V_{{\rm{Leichtbenzin}}}}}} = \frac{1}{{2000}}\) besitzt.
Entnimm der Animation in Abb. 5 den Durchmesser \(d\) des Ölflecks.
Berechne damit den Flächeninhalt \(A\) des Ölflecks und daraus seine Dicke \(h\).
Bestimme unter der vereinfachenden Annahme, dass das Volumen des Ölsäuremoleküls (chemische Formel: C17H33COOH, d.h. ein Ölsäuremolekül besteht aus 54 Atomen) würfelförmig ist und aus lauter kleinen gleichgroßen würfelförmigen Atomen zusammengesetzt ist, näherungsweise den Durchmesser eines Atoms.
Lässt man bei obigem Versuch nicht nur einen sondern zwei Tropfen auf die Wasseroberfläche fallen, so bildet sich ein kreisförmiger Ölfleck mit dem Durchmesser von ca. \(23{,}0\,{\rm{cm}}\).
Erläutere, inwiefern dieses Versuchsergebnis die Annahme einer monomolekularen Ölsäureschicht stützt.