Atomarer Energieaustausch

1. Beim Zusammenstoß eines Elektrons, dessen kinetische Energie kleiner ist als die Ionisierungsarbeit, mit einem Gasmolekül wird das Elektron im allgemeinen reflektiert, erleidet dabei jedoch einen Energieverlust, der um so kleiner ist, je geringer die Elektronenaffinität des Gases ist. Im Falle eines Gases ohne Affinität zum Elektron (Anm.: dies ist zum Beispiel Quecksilberdampf) ist dieser Energieverlust unmeßbar klein.
2. Bei einem Zusammenstoß zwischen einem Elektron und einem Gasmolekül, welcher zur Ionisation führt, verliert das Elektron seine gesamte kinetische Energie.
3. Ist beim Zusammenstoß zwischen einem Elektron und einem Gasmolekül die kinetische Energie des Elektrons gleich oder größer als die Ionisierungsarbeit, so ist die Wahrscheinlichkeit, daß der Zusammenstoß zur Ionisation führt, nicht klein gegen 1.

. . . . Der zur endgültigen Messung der Ionisierungsspannung verwandte Apparat ist in der Fig. 1 dargestellt. D ist ein Platindraht, dessen mittleres Stück dünner ist und durch einen elektrischen Strom zum Glühen gebracht werden kann. N ist ein feines Platindrahtnetz, welches den Draht D im Abstand von 4 cm zylindrisch umgibt, und G eine zylindrische Platinfolie, welche von N einen Abstand von 1 bis 2 mm hatte. G war durch ein Galvanometer mit der Erde verbunden.. . . .

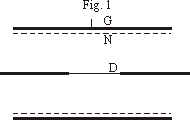
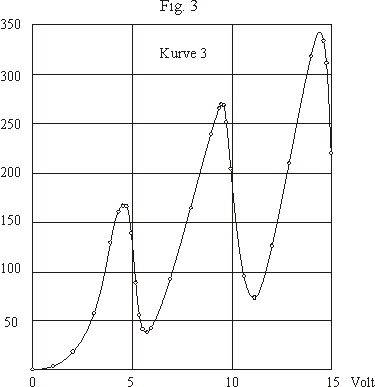
Während der Messung befand sich der Apparat in einem elektrisch geheizten Paraffinbad. Mit der während der Messungen dauernd laufenden Pumpe war er durch ein enges U-Rohr verbunden, das sich ebenfalls im Heizbad befand und an seinem tiefsten Punkt einen mit Quecksilber gefüllten Ansatz hatte. Da sich außerdem im unteren Teil des eigentlichen Apparates ein Tropfen Quecksilber befand, so wird der Druck des Quecksilberdampfes nicht wesentlich tiefer als der der Temperatur entsprechende Sättigungsdruck gewesen sein. Auf den genauen Wert des Druckes kommt es gar nicht an. Da die meisten Messungen bei Temperaturen von 110 bis 115° gemacht wurden, so betrug der Druck des Quecksilberdampfes etwa 1 mm.

. . . . . Um diesen Punkt (Anm.: wo die Ionisation einsetzt) noch genauer festzulegen, wurde nunmehr so verfahren, daß bei konstanter verzögernder Spannung zwischen N und G der am Galvanometer gemessene Strom in seiner Abhängigkeit von der zwischen D und N angelegten beschleunigenden Spannung gemessen wurde. Es ist folgender Verlauf zu erwarten: Solange die beschleunigende Spannung kleiner ist als die verzögernde, ist der Strom Null. Dann wird er ansteigen, bis die beschleunigende Spannung gleich der Ionisierungsspannung geworden ist. In diesem Augenblick werden die Elektronen in der Nähe des Drahtnetzes unelastische Stöße erleiden und dabei ionisieren. Da sie selbst und die bei der Ionisation befreiten Elektronen bis zum Durchtritt durch das Drahtnetz nur noch eine sehr geringe Spannung durchlaufen, so treten sie ohne merkliche Geschwindigkeit durch das Drahtnetz hindurch und sind nicht imstande, gegen das verzögernde Feld anzulaufen. Der Galvanometerstrom wird daher auf Null abfallen, sobald die beschleunigende Spannung größer geworden ist, als die Ionisierungsspannung. Steigert man die beschleunigende Spannung weiter, so rückt die Stelle, an der die Elektronen unelastische Stöße erleiden, vom Drahtnetz nach innen. Die nach dem unelastischen Zusammenstoß vorhandenen Elektronen durchlaufen also auf dem Wege zum Drahtnetz eine Spannung, welche gleich der Differenz der beschleunigenden Spannung und der Ionisierungsspannung ist. Sobald diese Differenz größer geworden ist, als die konstante verzögernde Spannung zwischen N und G, können wieder Elektronen gegen das verzögernde Feld anlaufen und der Galvanometerstrom steigt wieder an. Da die Zahl der Elektronen durch die Ionisation vergrößert ist, steigt er noch höher an, als das erste Mal. Sobald jedoch die beschleunigende Spannung gleich der doppelten Ionisierungsspannung geworden ist, erleiden die Elektronen in der Nähe des Drahtnetzes zum zweitenmal unelastische Zusammenstöße. Da sie hierbei ihre Energie ganz verlieren, die neugebildeten Elektronen ebenfalls keine merkliche Geschwindigkeit besitzen, so können keine Elektronen mehr gegen das verzögernde Feld anlaufen. Sobald daher die beschleunigende Spannung größer wird, als das Doppelte der Ionisierungsspannung, sinkt der Galvanometerstrom wieder auf Null. Da sich dieselbe Erscheinung jedesmal wiederholt, wenn die beschleunigende Spannung gleich einem ganzen Vielfachen der Ionisierungsspannung wird, so haben wir eine Kurve zu erwarten, die Maxima von wachsender Größe besitzt, deren Abstand stets gleich der Ionisierungsspannung ist.

. . . . . Die in den Kurven dargestellten Ergebnisse unserer Messungen zeigen, daß unsere Erwartungen sich durchaus bestätigt haben. Die Maxima sind außerordentlich scharf ausgeprägt und geben daher die Möglichkeit einer sehr genauen Messung der Ionisierungsspannung. Die Werte für den Abstand zweier benachbarter Maxima liegen sämtlich zwischen 4,8 und 5,0 Volt, so daß wir 4,9 Volt als den richtigsten Werte für die Ionisierungsspannung des Quecksilberdampfes ansehen können. . . . .