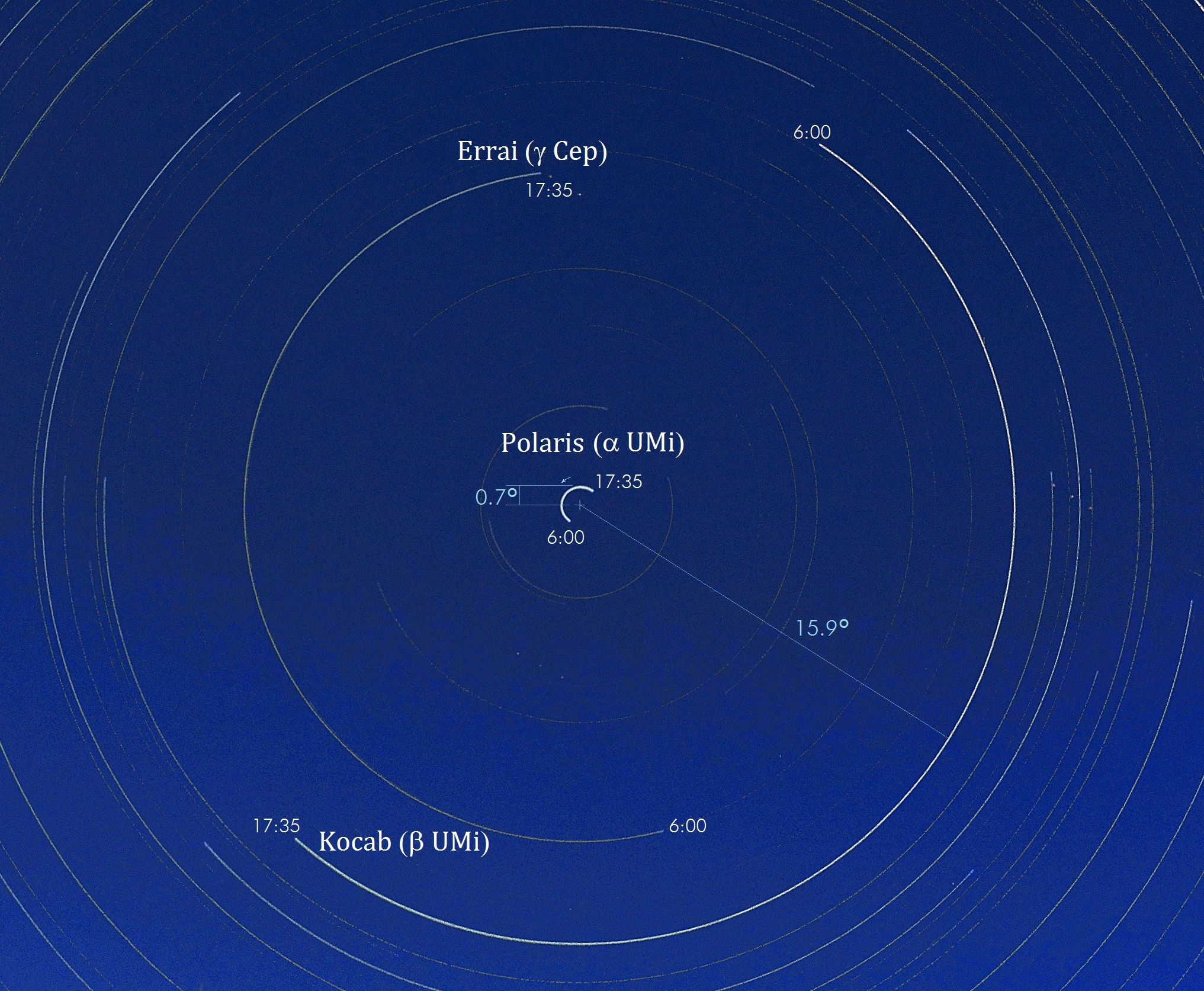
Sternenbewegung bei Langzeitbelichtung
Stellt man einen Fotoapparat auf ein feststehendes Stativ und fotografiert bei klarem Nachhimmel mit einer Belichtungszeit von mehreren Stunden, so ergibt sich ein Bild wie in Abb. 1. Alle Sterne zeichnen Kreisbögen mit unterschiedlichen Radien um den Polarstern im Kreiszentrum. Die Mittelpunktswinkel der Kreisbögen sind alle gleich und lassen sich aus der Belichtungszeit berechnen.
Historische Vermutungen zur Sternenbewegung
HERAKLID von Pontos (388-315 v. Chr.) vermutete als erster, dass die scheinbare tägliche Bewegung der Gestirne auf die Erdrotation zurückzuführen ist.
PLATON (427-347 v. Chr.), ARISTOTELES (383-322 v. Chr.), HIPPARCH (190-125 v. Chr.) und PTOLEMÄUS (87-170 n. Chr.) erklären die Sphären als um die Erde kreisende Kristallkugeln. HIPPARCH führte die Epizyklen der Planetenbahnen ein.
Lauf der Gestirne
Sterne, die nördlich der Äquatorebene sind, für die also die Deklination \(\delta>0\) ist, gehen im Nordosten auf und im Nordwesten unter. Dies ist in Abb. 2 zu sehen.
Sterne, die südlich des Äquators sind, für die also die Deklination \(\delta<0\) ist, gehen im Südosten auf und im Südwesten unter. In Abb. 3 wird dies veranschaulicht.
Der Merksatz, dass Sterne, Planeten, Sonne und Mond im Osten auf und im Westen untergehen, ist also nur für einen Beobachter in der Äquatorebene richtig. Liegt der Beobachtungspunkt ober- oder unterhalb der Äquatorebene, ist er nicht korrekt.
Obere und untere Kulmination
Jedem Stern kann eine Sternbahn zugeordnet werden. Diese Bahn besitzt zwei Schnittpunkte mit dem Himmelsmeridian: die untere und obere Kulmination. Die obere Kulmination beschreibt die größte Höhe und ist in Abb. 4 mit \(h_{o}\) eingezeichnet. Die geringste Höhe \(h_{u}\) wird als untere Kulmination bezeichnet.
Die Differenz zur Äquatorebene wird mit \(h_{ä}\) und die Polhöhe mit \(\varphi\) beschrieben.
Es gilt: \[ h_{o} = \delta + h_{ä} \] und \[ h_{u} = \delta - h_{ä} \]
wegen \( h_{ä} = 90^\circ - \varphi \) gilt
\[ \begin{array}{} h_{o} = \delta + \left( 90^\circ - \varphi \right) \\ \, \\
h_u = \delta - \left( 90^\circ - \varphi \right) \end{array} \]
Zirkumpolarsterne
Zirkumpolarsterne sind Sterne, die sich immer über der Horizontebene befinden. Ob ein Stern zirkumpolar ist, hängt davon ab, von welchem Standpunkt aus man die Sterne beobachtet:
- Am geographischen Pol sind alle sichtbaren Sterne zirkumpolar und sonst keine sichtbar.
- Am Erdäquator gibt es keine zirkumpolaren Sterne, keine unsichtbaren Sterne, alle sind zeitweilig sichtbar.
Aus der Position über der Horizontalebene folgt, dass die untere Kulmination positiv und die obere Kulmination negativ ist. Somit kann für den Zusammenhang, zwischen \(\delta \) und \(\varphi\) geschrieben werden.
\( h_{u} > 0 \Rightarrow \delta > 90^\circ - \varphi \)
Sterne, die hingegen immer unter der Horizontebene sind, sind nie sichtbar:
\( h_{o} < 0 \Rightarrow \delta < - \left( 90^\circ - \varphi \right) \)
Sterne mit \( - \left( 90^\circ - \varphi \right) < \delta < 90^\circ - \varphi \) sind zeitweise sichtbar.
Zeiten und Winkel
Die Zeit seit seiner oberen Kulmination (Südrichtung) ist der Stundenwinkel t eines Gestirns. Der Winkel von Norden bis zum Fußpunkt des Sterns ist der Azimut A. Es gilt nicht A + 180° = t (in Grad umgerechnet)!
Sternspuren
Die folgende Simulation veranschaulicht den vermeintlichen Lauf der Sterne an der Himmelskugel, welcher durch die Rotation der Erde verursacht wird. Oben links kannst du die Position des Beobachters auf der Erde auswählen. Neben der Wahl vorgegebener Orte kannst du auch eigene Koordinaten mit Länge und Breite angeben. Die "karierte Kugel" oberhalb der Erde stellt den sichtbaren Teil des Himmels dar. Hier kannst du das genutzte Koordinatensystem mit den Auswahlbuttons links wählen. Die unteren Einstellungen ermöglichen dir die Größe des Sichtfeldes zu variieren. Bei Wahl der Option geostationär wandert die Kameraperspektive exakt mit der Erddrehung, die Teleskop-Ansicht setzt den Beobachter auf die gewählten Koordinaten auf der Erde.
Oben rechst kannst du den zu beobachtende Stern auswählen oder die Position des gewünschten Sternes eingeben. Auch eine Suche nach Koordinaten von Sternen in der SIMBAD-Datenbank ist möglich. Unten rechts kannst du das gewünschte Beobachtungsdatum einstellen.
Wenn du nun den unteren Schieberegler für die Tageszeit (UTC) hin und her verschiebst, kannst du den Verlauf der roten Verbindungslinie zwischen dem Beobachter und dem beobachteten Stern betrachten. Der Kreisbogen auf der Himmelskugel ist der Lauf des Sterns.