Prinzip
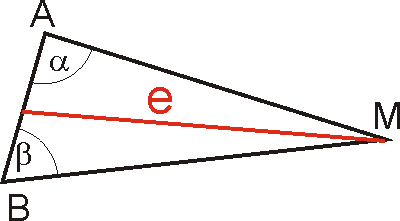
Eine Möglichkeit der Entfernungsbestimmung in der Astronomie besteht in der sogenannten Triangulation. Dazu peilt man von zwei Punkten A und B aus den Punkt M, dessen Entfernung e man wissen will, an und bestimmt die Winkelweiten α und β. Mit Sätzen der Ebenen Trigonometrie (z.B. Sinus- und Cosinussatz) lässt sich dann e bestimmen. Die Entfernungsbestimmung wird eine brauchbare Genauigkeit haben, wenn die Länge der Messbasis [AB] nicht verschwindend klein gegenüber der Entfernung e ist.
Bestimmung der Entfernung Erde-Mond
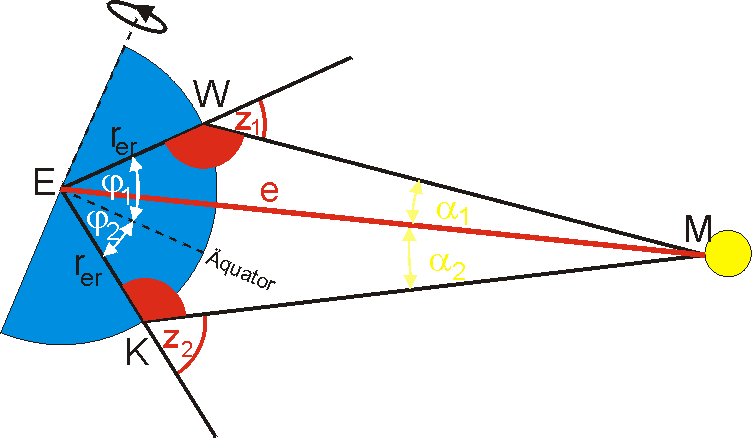
Von zwei möglichst weit entfernten Punkten der Erdkugel (z.B. Wien mit der nördlichen geografischen Breite \({\varphi _1} = 48^\circ 15'\) und Kapstadt mit der südlichen Breite \({\varphi _2} = 33^\circ 58'\)), die in etwa auf gleicher geographischer Länge liegen, wird ein bestimmter Punkt des Mondes angepeilt. Dabei hat man folgende Winkel zur Zenitrichtung gemessen: Wien \({z_1} = 27^\circ 40'\) und Kapstadt \({z_2} = 55^\circ 43'\).
Theorie
Die Winkelsumme im Viereck EKMW ist \(360^\circ \) bzw. im Bogenmaß \(2\pi \). Also gilt
\[{\varphi _1} + {\varphi _2} + \left( {180^\circ - {z_1}} \right) + \left( {180^\circ - {z_2}} \right) + {\alpha _1} + {\alpha _2} = 360^\circ \]
bzw. im Bogenmaß (mit dem wir jetzt weiterarbeiten)
\[{\varphi _1} + {\varphi _2} + \left( {\pi - {z_1}} \right) + \left( {\pi - {z_2}} \right) + {\alpha _1} + {\alpha _2} = 2\pi \]
Daraus ergibt sich
\[{\alpha _1} + {\alpha _2} = {z_1} + {z_2} - {\varphi _1} - {\varphi _2}\quad(1)\]
Mit Hilfe des Sinus-Satzes können nun die unbekannten Winkelweiten \({\alpha _1}\) bzw. \({\alpha _2}\) bestimmt werden.
Im Dreieck EMW gilt
\[\frac{{\sin \left( {{\alpha _1}} \right)}}{{\sin \left( {\pi - {z_1}} \right)}} = \frac{{{r_{er}}}}{e} \Leftrightarrow \sin \left( {{\alpha _1}} \right) = \frac{{{r_{er}}}}{e} \cdot \sin \left( {\pi - {z_1}} \right)\]
entsprechend gilt im Dreieck EKM
\[\frac{{\sin \left( {{\alpha _2}} \right)}}{{\sin \left( {\pi - {z_2}} \right)}} = \frac{{{r_{er}}}}{e} \Leftrightarrow \sin \left( {{\alpha _2}} \right) = \frac{{{r_{er}}}}{e} \cdot \sin \left( {\pi - {z_2}} \right)\]
Da \(\sin \left( {\pi - {z_1}} \right) = \sin \left( {{z_1}} \right)\) ist und für kleine Winkel \({\alpha _1}\) gilt \({\alpha _1} \approx \sin \left( {{\alpha _1}} \right)\) (entsprechendes gilt für \({z_2}\) und \({\alpha _2}\)), folgt:
\[{\alpha _1} = \frac{{{r_{er}}}}{e} \cdot \sin \left( {{z_1}} \right)\]
und entsprechend
\[{\alpha _2} = \frac{{{r_{er}}}}{e} \cdot \sin \left( {{z_2}} \right)\]
Setzt man diese Beziehungen in (1) ein und löst die Gleichung nach der Variablen \(e\) auf, so ergibt sich
\[e = {r_{er}} \cdot \frac{{\sin \left( {{z_1}} \right) + \sin \left( {{z_2}} \right)}}{{{z_1} + {z_2} - {\varphi _1} - {\varphi _2}}}\]
wobei noch einmal gesagt werden soll, dass hier alle Winkelweiten im Bogenmaß einzusetzen sind.
Aufgabe: Entfernungsmessung Erde-Mond mit Triangulation
Bestimme mit den obigen Daten von Wien und Kapstadt, um wie viel mal größer die Entfernung Erde-Mond im Vergleich zum Erdradius ist.

