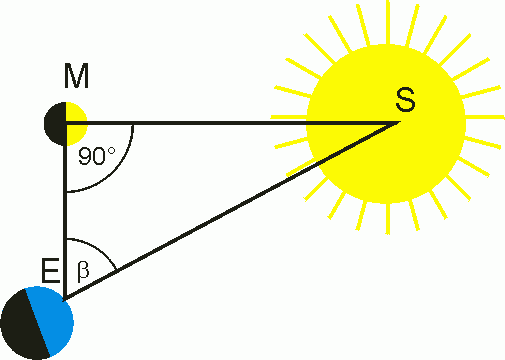
Prinzip der Triangulation
Hinweis: In der Astronomie wird die Entfernung Erde-Sonne von ca. 150 Millionen Kilometern als astronomische Einheit (AE) bezeichnet. Man drückt die Entfernungen anderer Planeten meist in Vielfachen der astronomischen Einheit aus. Die Methode der Triangulierung geht wohl auf Aristarch von Samos (250 v. Chr.) zurück, der mit dieser Methode die Entfernung Erde-Sonne abschätzte. Als Basis der Triangulierung verwendete er die Strecke Erde-Mond und bestimmte den Winkel \(\beta\) (vgl. Skizze) gerade dann, wenn von der Erde aus Halbmond beobachtet wurde. In diesem Fall ist der Winkel bei M nämlich 90°. Somit gilt im Dreieck EMS
\[\cos \left( \beta \right) = \frac{{\left| {\overline {{\rm{EM}}} } \right|}}{{\left| {\overline {{\rm{ES}}} } \right|}}\]
Aristarch hat mit seinen wenigen Hilfsmitteln einen Winkel von \(\beta=87^{\circ}\) gemessen.
Aufgabe
Bestimme aus der Winkelmessung des Aristarch das Verhältnis von Sonnen- zu Mondentfernung.
Mit modernen Methoden stellt man für \(\beta\) einen Wert von \(89^{\circ}51'\) (89 Grad und 51 Bogenminuten) fest. Eine Bogenminute ist dabei der sechszigste Teil eines Grades ist. Somit ergibt sich der Winkel \(\beta\) in Grad zu \(\beta=89^{\circ}+51'=89^{\circ}+\frac{51}{60}^{\circ}=89{,}85^{\circ}\).
a) Bestimme mit diesem genauen Wert noch einmal das Verhältnis von Sonnen- zu Mondentfernung.
b) Vergleiche das Ergebnis mit den Ergebnissen von Aristarch.