Aus dem 3. Keplerschen Gesetz \(\frac{{{T_1}^2}}{{{T_2}^2}} = \frac{{{a_1}^3}}{{{a_2}^3}}\) kann man auch bei bekannten Umlaufzeiten \(T\) nur die Verhältnisse von Entfernungen zueinander bestimmen. Die wahren Entfernungen können jedoch so nicht berechnet werden. So wusste man zwar früh, dass der die Entfernung der Venus von der Sonne \(0{,}723\,\rm{AE}\), also 0,73-mal den Abstand zwischen Sonne und Erde, beträgt, konnte aber keine genaue Entfernungsangabe in Kilometern geben.
Halley Methode zur Bestimmung von Entfernungen
Der Brite Edmon Halley schlug 1716 als erstes eine Methode vor, mit der man Entfernungen im Sonnensystem bestimmen kann. Dazu sollten ein Beobachter weit im Norden (z.B. London) und ein Beobachter weit im Süden (z.B. Kapstadt) jeweils den Venusdurchgang vor der Sonne beobachten. Aufgrund der unterschiedlichen Position der beiden Beobachter im Abstand \(d\), nehmen sie die Venus auch an unterschiedlichen Positionen der Sonne wahr und messen unterschiedlich lange Durchgangszeiten (siehe Abb. 1). Von Kapstadt aus ist die Venus näher am oberen Rand der Sonne zu sehen und daher für den Beobachter hier auch eine kürzere Zeit vor der Sonne. Der Beobachter in London sieht die Venus weiter in der Mitte der Sonne und daher auch länger.
Bestimmung der Entfernung zwischen den beobachteten Venusdurchgängen
Aus den genauen Beobachtungen des Venusdurchgangs (insbesondere von den Zeiten des Durchgangs) von beiden Orten aus und den bekannten relativen Entfernungen Erde-Sonne bzw. Venus-Sonne, kann dann über die Ähnlichkeit zweier Dreiecke die Entfernung \(D\) zwischen den wahrgenommenen Venusdurchgängen auf der Sonne berechnet werden.
Bestimmung der Länge einer Astronomischen Einheit
Aus den Versuchsergebnissen kann auch der Winkel \(\delta\) bestimmt werden, unter dem man von London aus zwei Punkte auf der Sonne in der Distanz \(D\) sehen würde. Es ergibt sich ein Winkel von \(\delta = 30''\) wobei \(30´´\approx 0{,}0083^{\circ}\) sind. Aus geometrischen Überlegungen folgt damit: \[{tan\left( {\frac{\delta }{2}} \right) = \frac{{\frac{D}{2}}}{{1{\rm{AE}}}} \Leftrightarrow 1{\rm{AE}} = \frac{{\frac{D}{2}}}{{tan\left( {\frac{\delta }{2}} \right)}}}\]
Einsetzen der aus den Beobachtung gewonnenen Werten liefert \[\rm{AE} = \frac{\frac{2{,}20 \cdot 10^7 \rm{m}}{2}}{\tan\left( \frac{0{,}0083^{\circ}}{2}\right)} = 1{,}5 \cdot {10}^{11}\,\rm{m}\]
Probleme bei der Genauigkeit
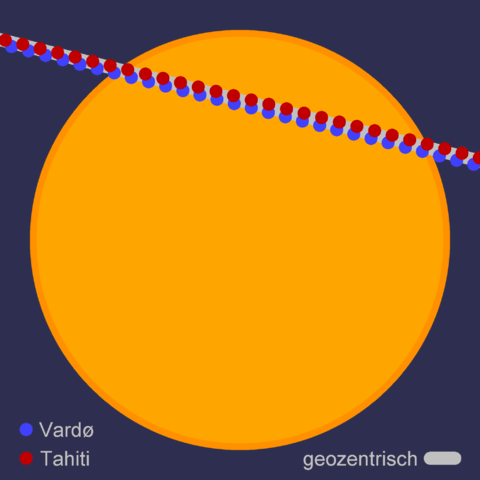
Bei den Venusdurchgängen 1761, 1769, 1874 und 1882 wurden diverse Messungen an verschiedenstern Orten der Erde nach den Ideen Halleys, der schon 1742 verstarb, durchgeführt. Die Ergebnisse waren jedoch nicht befriedigend genau. Wie in Abb. 4 zu sehen sind die real zu beobachtenden Abstände und Zeitunterschiede gering.
Später wurden Messungen mit dem Asteroiden Eros durchgeführt, der im Jahr 1930 nur 0,15 AE von der Erde entfernt war. Dies lieferte bessere Ergebnisse.
Noch genauere Daten ergeben Radarreflektionszeitmessungen zu Mars und Venus, die seit 1960 durchgeführt werden.