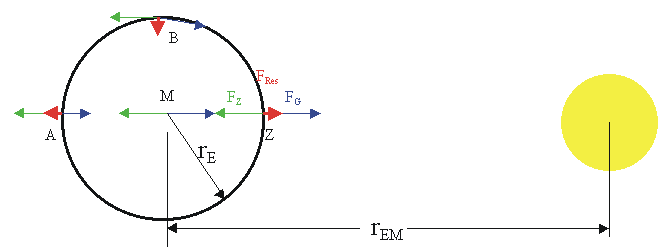
In Mittelpunkt \(M\) der Erde beträgt der Betrag der Gravitationskraft
\[{F_{{\rm{G}}{\rm{,M}}}} = G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{r_{{\rm{EM}}}}^2}}\]
und ist dort dem Betrag \({F_{{\rm{ZF}}}}\) der Zentrifugalkraft gleich. An allen anderen Punkten der Erde hat die Zentrifugalkraft aber auch diesen Wert, d.h. es gilt
\[{F_{{\rm{ZF}}}} = G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{r_{{\rm{EM}}}}^2}}\]
Im Punkt A gilt
\[{F_{{\rm{G,A}}}} = G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2}}}\]
und damit für den Betrag der resultierenden Kraft
\[{F_{{\rm{res}}{\rm{,A}}}} = G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{r_{{\rm{EM}}}}^2}} - G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2}}} = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \left( {\frac{1}{{{r_{{\rm{EM}}}}^2}} - \frac{1}{{{{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2}}}} \right)\]
Bringt man die Brüche in der Klammer auf einen gemeinsamen Nenner und subtrahiert sie dann voneinander, so ergibt sich
\[{F_{{\rm{res}}{\rm{,A}}}} = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \left( {\frac{{{{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2} - {r_{{\rm{EM}}}}^2}}{{{r_{{\rm{EM}}}}^2 \cdot {{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2}}}} \right) = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \frac{{{r_{{\rm{EM}}}}^2 + 2 \cdot {r_{{\rm{EM}}}} \cdot {r_{\rm{E}}} + {r_{\rm{E}}}^2 - {r_{{\rm{EM}}}}^2}}{{{r_{{\rm{EM}}}}^2 \cdot {{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2}}} = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \frac{{2 \cdot {r_{{\rm{EM}}}} \cdot {r_{\rm{E}}} + {r_{\rm{E}}}^2}}{{{r_{{\rm{EM}}}}^2 \cdot {{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2}}}\]
Klammert man schließlich im Zähler \({{r_{\rm{E}}}}\) aus, so erhält man
\[{F_{{\rm{res,A}}}} = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \frac{{{r_{\rm{E}}} \cdot \left( {2 \cdot {r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}}{{{r_{{\rm{EM}}}}^2 \cdot {{\left( {{r_{{\rm{EM}}}} + {r_{\rm{E}}}} \right)}^2}}}\]
Nun kann man wegen \({{r_E} \ll {r_{EM}}}\) die Näherungen \({2 \cdot {r_{{\rm{EM}}}} + {r_{\rm{E}}} \approx 2 \cdot {r_{{\rm{EM}}}}}\) sowie \({{r_{{\rm{EM}}}} + {r_{\rm{E}}} \approx {r_{{\rm{EM}}}}}\) anwenden und erhält
\[{F_{{\rm{res}}{\rm{,A}}}} \approx G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \frac{{{r_{\rm{E}}} \cdot 2 \cdot {r_{{\rm{EM}}}}}}{{{r_{{\rm{EM}}}}^2 \cdot {r_{{\rm{EM}}}}^2}} = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \frac{{2 \cdot {r_{\rm{E}}}}}{{{r_{{\rm{EM}}}}^3}}\]
Entsprechend gilt für den Punkt Z
\[{F_{{\rm{G,Z}}}} = G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{{\left( {{r_{{\rm{EM}}}} - {r_{\rm{E}}}} \right)}^2}}}\]
sowie
\[{F_{{\rm{res,Z}}}} = G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{r_{{\rm{EM}}}}^2}} - G \cdot \frac{{{m_{\rm{E}}} \cdot {m_{\rm{M}}}}}{{{{\left( {{r_{{\rm{EM}}}} - {r_{\rm{E}}}} \right)}^2}}} = ... = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \frac{{{r_{\rm{E}}} \cdot \left( {2 \cdot {r_{{\rm{EM}}}} - {r_{\rm{E}}}} \right)}}{{{r_{{\rm{EM}}}}^2 \cdot {{\left( {{r_{{\rm{EM}}}} - {r_{\rm{E}}}} \right)}^2}}}\]
Die entsprechenden Näherungen wie oben liefern
\[{F_{{\rm{res,Z}}}} = G \cdot {m_{\rm{E}}} \cdot {m_{\rm{M}}} \cdot \frac{{2 \cdot {r_{\rm{E}}}}}{{{r_{{\rm{EM}}}}^3}}\]
Die Gezeitenkräfte sind also indirekt proportional zur dritten Potenz des Abstands der Körper und wirken auf der dem Mond zugewandten und der dem Mond abgewandten Seite jeweils vom Erdmittelpunkt weg.

