Auf Basis der Verteilung von Galaxien im Weltall und ihrer Rotverschiebung stellte der Belgier Georges LEMAÎTRE 1927 die Theorie auf, dass sich unser Universum ausdehnt. Wie die Rosinen in einem Hefeteig sollten sich die Galaxien mit der Expansion des Universums immer weiter und schneller auseinanderbewegen, wobei der Vergleich mit dem Hefeteig nicht ganz richtig ist, da der Hefeteig eine Mitte hat, das Universum aber nicht.
Edwin HUBBLE lieferte 1929 hierzu passende Daten, die eine Regelmäßigkeit in der Bewegung der Galaxien zeigten: Galaxien entfernen sich um so schneller von uns, je weiter die Galaxien von uns weg sind.
HUBBLE-Konstante bzw. HUBBLE-Parameter
Aufgrund von HUBBLEs Beobachtungen nahm man zunächst an, dass die Rotverschiebung \(z\) bzw. die "Fluchtgeschwindigkeit" \(v\) einer Galaxie direkt proportional zu ihrer Entfernung \(D\) zu uns ist. Mit der als HUBBLE-Konstanten bezeichneten Proportionalitätskonstanten \(H\) konnte diese Beziehung zwischen Entfernung und Rotverschiebung (bzw. "Fluchtgeschwindigkeit") mit der Gleichung \[z\cdot c=H\cdot D\] ausgedrückt werden. Diese Gesetzmäßigkeit nennt man das HUBBLE-LEMAÎTRE-Gesetz.
Später stellte man jedoch fest, dass sich die Expansion des Universums beschleunigt. Daher ändert sich der Wert von \(H\) im Laufe der Zeit. \(H\) ist also zeitabhängig und nicht konstant. Es wird eigentlich \(H(t)\) notiert werden. Entsprechend wird die Größe inzwischen häufig auch korrekterweise als HUBBLE-Parameter bezeichnet. Die lineare Beziehung \(z\cdot c=H_0\cdot D\) gilt nur für Rotverschiebungen bis \(z\approx 0{,}1\), was etwa auf Objekte in einer Entfernung von 400 Mpc zutrifft.
Als HUBBLE-Konstante \(H_0\) bezeichnet man dabei die aktuelle Expansionsrate des Universums. Die HUBBLE-Konstante beträgt aktuell: \[H_0\approx 70\,\rm{\frac{km}{s\cdot Mpc}}\] Je nach Messmethode variiert dieser Wert etwas.
"Fluchtgeschwindigkeiten" mit dem HUBBLE-LEMAÎTRE-Gesetz
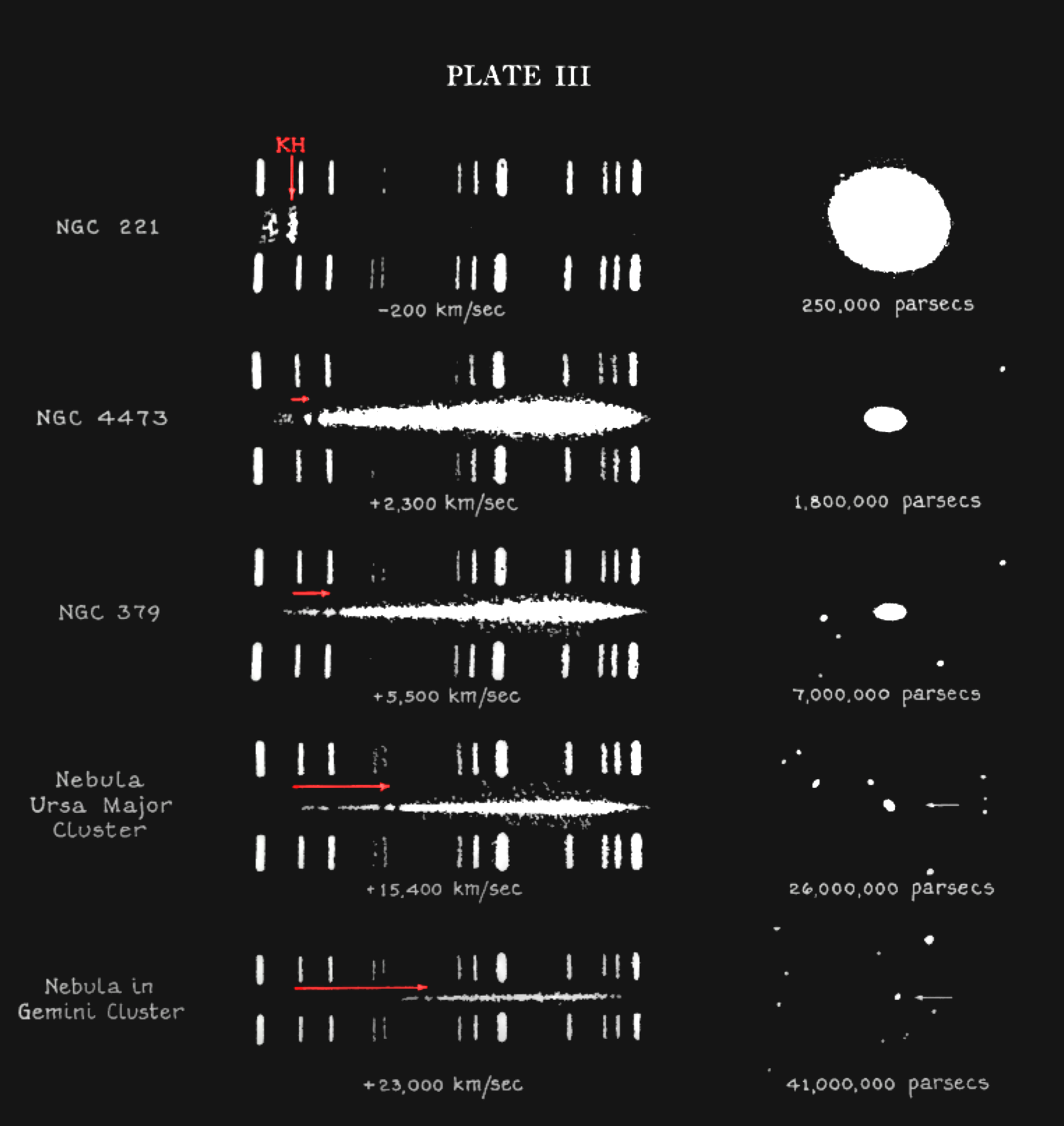
Im Bild sieht man die Rotverschiebungen der H- und K-Linie verschiedener Galaxien.
Interpretiert man die aus der gemessenen Rotverschiebung \(z\) mittels \(v=c\cdot z\) berechnete Geschwindigkeit \(v\) im Sinne des Dopplereffektes, so kann man aus dem Hubble-Lemaître-Gesetz die "Fluchtgeschwindigkeit" \(v_{\rm{Flucht}}\) einer Galaxie in einer Entfernung \(D\) bestimmen. Für \(v_{\rm{Flucht}}\) einer Galaxie in der Entfernung \(D\) gilt: \[v_{\rm{Flucht}}\approx H_0\cdot D\]
Diese Beziehung gilt jedoch nur, solang man \(H_0\) als nahezu konstant ansehen kann. Die genaue Beziehung zwischen Rotverschiebung und Entfernung ist nichtlinear und erfordert eine Integration über den sog. Skalenfaktor \(a(t)\) des Universums, der die relative Expansion des Universums im Laufe der Zeit beschreibt.
Aufgabe
Bei einer Galaxie wird die Hα-Linie des Wasserstoffs - im Labor eine scharfe Linie bei \(\lambda_{0}= 656{,}297\,\rm{nm}\) - verschoben bei der Wellenlänge \(\lambda_{1}=658{,}003\,\rm{nm}\) beobachtet.
Mit welcher Geschwindigkeit und welcher Richtung bewegt sich die Galaxie und wie weit ist sie entfernt, wenn als Hubblekonstante \(H_0=70\,\rm{\frac{km}{s\cdot Mpc}}\) angenommen wird.