Die Cepheiden sind veränderliche Sterne, die nach dem Stern δ Cephei; im Sternbild Cepheus benannt sind, eine Unterklasse der Pulsationsveränderlichen. Cepheiden verändern ihre Leuchtkraft streng periodisch, dabei verändert sich auch ihre Spektralklasse und somit ihre Oberflächentemperatur.
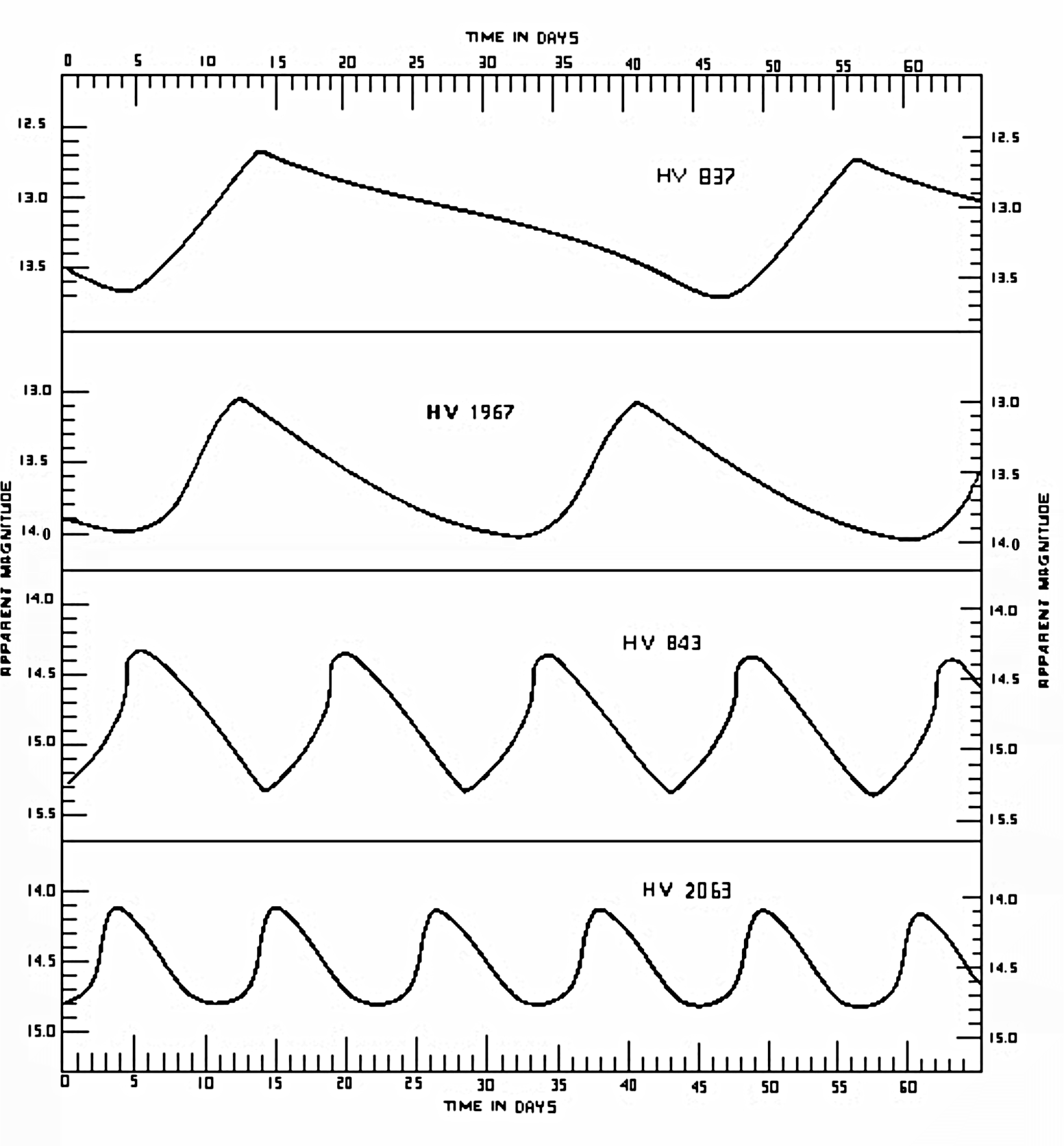
1912 untersuchte Henrietta Swan LEAVITT (1868 - 1921) am Harvard College Observatorium Fotoplatten mit Aufnahmen der sehr hellen pulsierenden Sterne in der kleinen Magellanschen Wolke (Abb. 1). Sie fand dabei heraus, dass die Helligkeiten einer Gruppe von 25 Sternen in der kleinen Magellanschen Wolke, die dem Stern \(\delta\)-Cephei gleichen, mit ihrer Periode in Zusammenhang stehen.
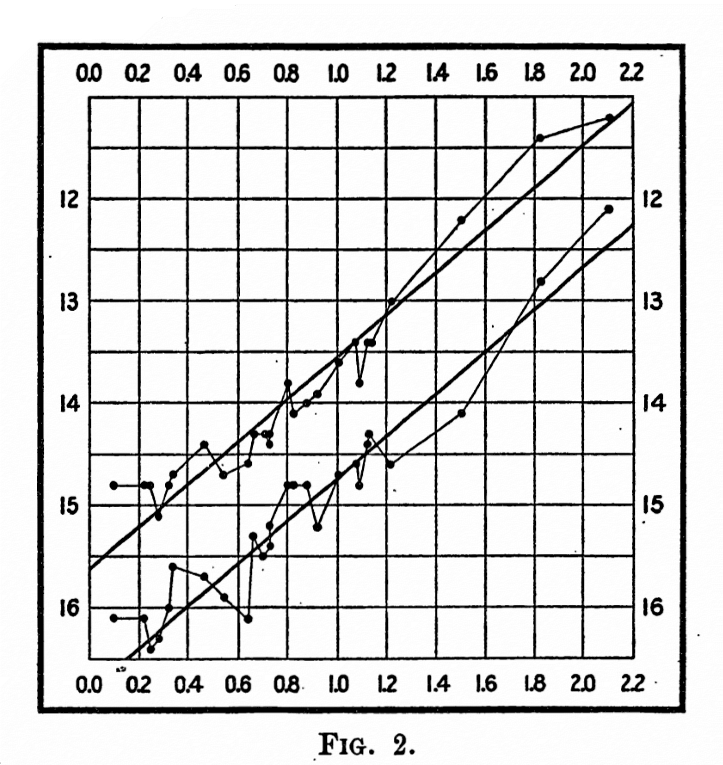
Geraden bei doppelt logarithmischem Maßstab
Im doppelt logarithmischen Maßstab (nach oben aufgetragen die relative Helligkeit) nach rechts der Logarithmus der Periode ergaben sich sowohl für das Strahlungsmaximum und das Strahlungsminimum parallele Geraden, wie die rechte, von Pickering 1912 veröffentlichte Grafik zeigt.
Daraus ergibt sich folgende Gesetzmäßigkeit für die mittlere relative Helligkeit m und Periode p gleichweit entfernter Cepheiden:
\[\frac{{{p_1}}}{{{p_2}}} = {10^{\frac{{{m_2} - {m_1}}}{{2,54}}}} \Rightarrow \lg \frac{{{p_1}}}{{{p_2}}} = \frac{{{m_2} - {m_1}}}{{2,54}} \Rightarrow {m_1} = {m_2} - 2,54 \cdot \lg \frac{{{p_1}}}{{{p_2}}}\]
Rückschluss auf die absolute Helligkeit
Da alle Sterne der kleinen Magellanschen Wolke von uns aus gesehen gleich weit entfernt sind, gilt diese Formel natürlich in gleicher Weise auch für absolute Helligkeiten. Um die Formel aber auf absolute Helligkeiten zu "eichen" benötigte man einen Cepheiden, dessen Entfernung und damit seine absolute Helligkeit kannte. Dies gelang 1919 Harlow Shapley mit Cepheiden aus Kugelsternhaufen unserer Galaxie.
Wodurch die Pulsationsveränderung kommt, zeigt die Seite Pulsationsveränderliche.
Entfernungsbestimmung mit Cepheiden
Cepheiden sind recht häufige Riesensterne und sehr helle Objekte, die man von der Erde aus bis zu einer Entfernung von einigen Megaparsec, mit dem Hubble-Weltraumteleskop sogar bis zu Entfernungen von etwa 20 Megaparsec, beobachten kann. Das macht Cepheiden zu einem brauchbaren Mittel für die astronomische Entfernungsbestimmung: Aus der Periode eines Cepheiden, die man direkt beobachten kann, kann man auf seine absolute Helligkeit schließen. Durch den Vergleich mit der beobachteten relativen Helligkeit kann anschließend die Entfernung des Cepheiden von der Erde rein rechnerisch aus dem sog. Entfernungsmodul \(m-M=5 \cdot \lg \left( {\frac{r}{{10\,\rm{pc}}}} \right)\) bestimmt werden.
Standardkerzen
Als Standardkerze bezeichnet man in der Astronomie ein leuchtendes Objekt mit bekannter oder einfach berechenbarer absoluter Helligkeit. Mit Standardkerzen kann man entsprechend auf die Entfernung von Objekten schließen. In einem Bereich bis 20 Mpc sind Cepheiden geeignete Standardkerzen. Weitere Standardkerzen sind die RR-Lyrae-Sterne, die W-Virginis-Sterne und für sehr entfernte Objekte Supernovae vom Typ 1a.
Aufgabe
Verständnisaufgabe
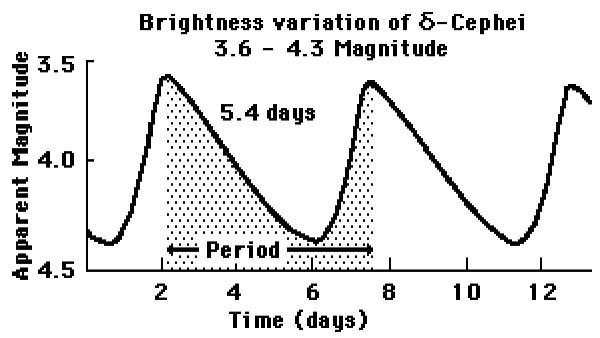
\(\delta\)-Cephei hat eine Periode von 5,4 Tagen. Seine relative Helligkeit schwankt wischen 3,6 und 4,3 Magnituden. Seine Entfernung beträgt \(r=313\,\rm{pc}\).
Berechne die mittlere absolute Helligkeit \(\rm{M_{\delta-Cephei}}\).
Leite eine Formel her, mit der man die absolute Helligkeit eines Cepheiden aus seiner Periode bestimmt.